-
Через точку А к данной окружности проведены касательная АВ (В - точка касания) и секущая AD , проходящая через центр О (D - точка на окружности, О лежит
между A и D). Найдите угол BAD и угол ADB, если дуга BD=110°20'
Объясните как решать, подробно.
Относительно этого рисунка.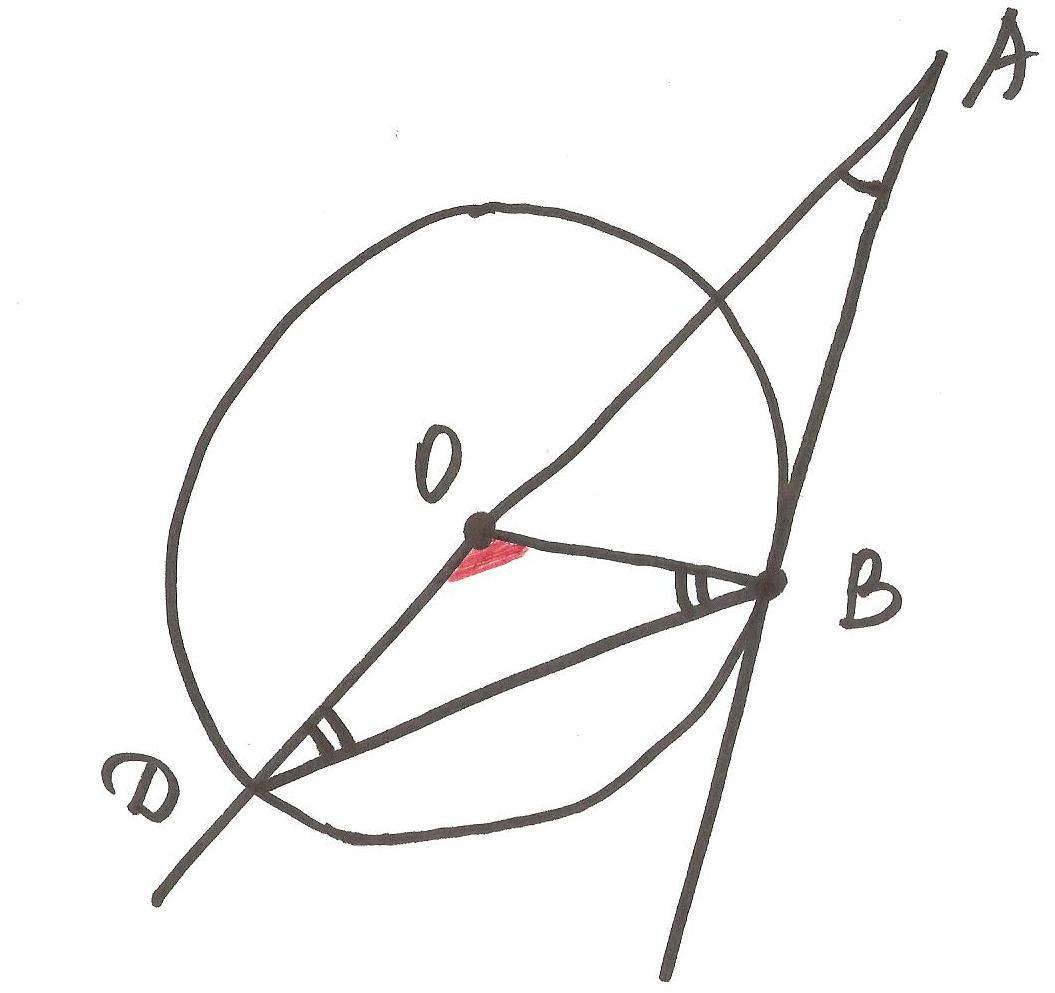
Ответы 1
-
Рассмотрим ΔДОВ: стороны ОД=ОВ (радиусы), значит углы при основании равны <ОДВ=<ОВД, <ДОВ - центральный угол, опирающийся на дугу ВД, значит <ДОВ=110°20'.Следовательно <ОДВ=<ОВД=(180-110°20')/2=34°50'Т.к. касательная к окружности перпендикулярна к радиусу, проведенному в точку касания, то <ОВА=90°.Рассмотрим ΔДАВ: <АДВ=<ОДВ=34°50' (совпадают), <АВД=<ОВА+<ОВД=90+34°50'=124°50'. Тогда <ВАД=180-<АДВ-<АВД=180-34°50'-124°50'=20°20'.Ответ: 20°20' и 34°50'
-
Автор:
kyla - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
чем гордились советские люди в 60-80 годы прошлого века?
-
Предмет:
Обществознание -
Автор:
kailynsg90 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
перепиши данные предложение , употребив глаголы в простом будущем времени. 1) Пробилась зелень полевая навстречу ветру и теплу. 2)Скользнула в воздухе
ласточка , мальчик посмотрел ей вслед. 3) Самолет поднялся выше облаков , и солнце опять засияло над нами на синем небе.-
Предмет:
Русский язык -
Автор:
dixiehays - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Найдите сумму чисел 60 и 40, 50 и 20. Найдите их разность
-
Предмет:
Математика -
Автор:
zackery - 6 лет назад
-
Ответов:
3 -
Смотреть
-
- перечислете природные зоны тропического, умепенного и полярного поясов , пустыню, тундру
How much to ban the user?
1 hour
1 day
100 years
