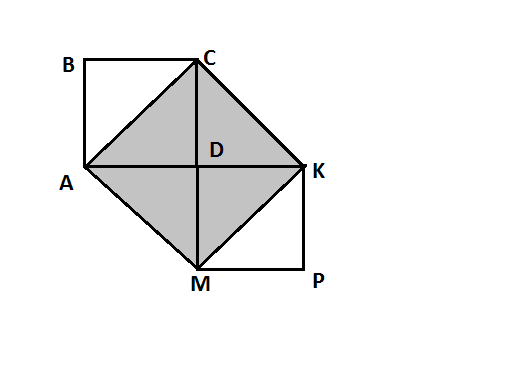
ABCD и MDKP - равные квадраты (рис.) AB=8 см.Найдите площадь и периметр четырёхугольника ACKM. (Полное решение задачи) - №1206150

ABCD и MDKP - равные квадраты (рис.) AB=8 см.Найдите площадь и периметр четырёхугольника ACKM.

(Полное решение задачи)
- Предмет:
  Геометрия
- Автор:
  victoriorvsj
- 5 лет назад

Ответы 1

Рассмотрим фигуру:

1. АВСD=MDKP- равные квадрату по условию, значит и элементы у них равны( в данном случае стороны): АВ=PK=8 см.

2. У квадрата по свойству все стороны равны, значит АВ=ВС=СD=DA=DM=MK=KP=PD=8 cм

3. Рассмотрим ромб АСКМ, та фигура с которой мы продолжим работать. У этой фигуры, скорее ромба, площадь выражается формулой:

$S=\frac{1}{2}*CM*AК/tex]</em></p> <p> </p> <p><em>[tex]S=\frac{1}{2}*16*16=128$ см $^{2}$

4. Идем дальше, периметр- сумма длин всех сторон, а значит P= AC+CK+KM+MA

Так как у этой фигуры равны пары элементов, то AC=CK=KM=MA.

Периметр, точнее вышенаписанные стороны, можно узнать через теорему Пифагора: $AC^{2}=AB^{2}+BC^{2}$ , тогда $8^{2}+8^{2}=?^{2} ?^{2}=128 ?= \approx11,3$

5. P=11.3*4= \approx45.2 cм .

Ответ: S=128 см $^{2}$

P= 45.2 cм .
- Автор:
  porcherspb
- 5 лет назад
- 0
Добавить свой ответ

Еще вопросы

How much to ban the user?

1 hour 1 day 100 years