-
В прямоугольной трапеции ABCD (AD‖BC, AB перпендикулярна CD) большее основание AD = 15 см, диагональ АС перпендикулярна CD, AC = 12 см. Найти меньшее основание
трапеции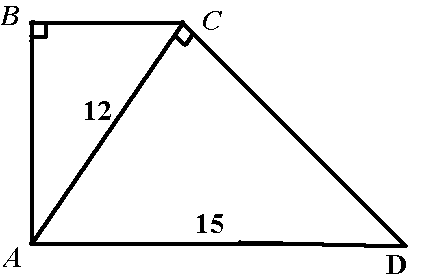
Ответы 1
-
ΔАСD: по теореме Пифагора AD²=AC²+CD²15²=12²+CD², CD=9 смCH - высота ΔACDпусть АН= х см, тогда НD=(15-x) смΔAHC: по теореме Пифагора АС²=СН²+АН², 12²=х²+СН². СН²=12²-х², СН²=144-х²ΔCHD: по теореме Пифагора CD²=CH²+HD², 9²=CH²+(15-x)², CH²=-144+30x-x²CH - общая сторона для ΔAHC и ΔDHC144-x²=-144+30x-x²30x=288x=9,6AH=BC=9,6ответ: меньшее основание трапеции =9, 6 см
-
Автор:
heavenlucas - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
три целых три пятых разделить на девять
-
Предмет:
Математика -
Автор:
champqm28 - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
установите соответствие между морем и океаном к которому оно относится: 1.атлантический океан,2.тихий океан,3.индийский океан,4.северный ледовитый океан. а.жёлтое море,б.белое море,в.чёрное море,г.красное море.
-
Предмет:
География -
Автор:
donovan677 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Как решить? 6*11^(log11(3))
-
Предмет:
Алгебра -
Автор:
bernardolong - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
скорость и время движения пешехода на участке 8 км - нужно определить вид зависимости
-
Предмет:
Математика -
Автор:
carina - 6 лет назад
-
Ответов:
0 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
