-
100 баллов . СЛОЖНАЯ ГЕОМЕТРИЯ
2 аналогичные задачи
Нужны точные ответы!!!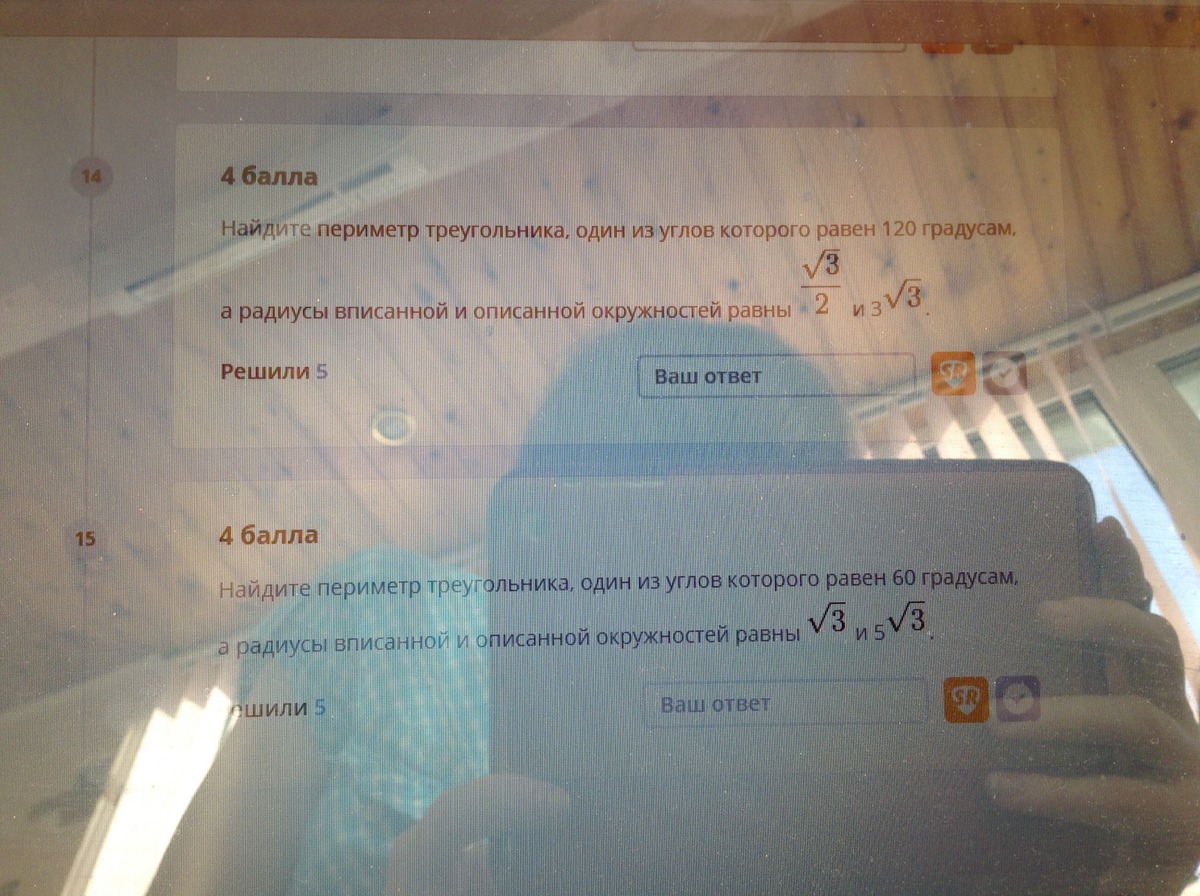
-
Предмет:
Геометрия -
Автор:
maximilianomaldonado - 6 лет назад
-
Ответы 6
-
досчитайте второе, подалуйста! нужно сверить!
-
Автор:
annutb3 - 6 лет назад
-
0
-
-
32 . но еще раз проверять , сегодня арифметическое устройство дает ужасные сбои .
-
Автор:
avaokoz - 6 лет назад
-
0
-
-
36 во втором?
-
Автор:
alex0j3w - 6 лет назад
-
0
-
-
да правильно с +(а+b) =15+21 =36 .
-
Автор:
mireyamcneil - 6 лет назад
-
0
-
-
14) c/sinC =2R ⇒c =2R*sin120° =2*3√3*√3/2 = 9;c² =a² +b² -2ab*cos120° =a² +b² +ab (1)S =(a+b+c)/2 *r ;1/2ab*sin120° =(a+b+9)/2*√3/2 √3/4 ab =(a+b+9)*3/4 ;ab =a+b+9 (2)------------------------------{ a² +b² +ab =81; ab =a+b+9 .{ (a +b)² - ab =81; ab =a+b+9 .⇔{(a+b)² -(a+b+9) =81 ; ab =a+b+9.(a+b)² -(a+b) -90 =0 ;a+b =10 ; *** a+b= -9*** =P =a+b+c =10+9 =19 .аналогично вторая:15) c/sinC =2R ⇒c =2R*sin60° =2*5√3*√3/2 = 15;c² =a² +b² -2ab*cos60° =a² +b² - ab (1)S =(a+b+c)/2 *r ;1/2ab*sin60° =(a+b+15)/2*√3 ; √3/4 ab =(a+b+15)*√3/2 ;ab =2(a+b)+30 (2)------------------------------------------------------------------------------------------{ a² +b² +ab =225 ; ab =2(a+b)+30 .{ (a +b)² - 3ab =225 ; ab =2(a+b)+30 .⇔{(a+b)² -6(a+b) -90 =225 ; ab =2(a+b)+30.(a+b)² -6(a+b) -315=0 ;a+b =21 ; *** a+b= -15***=P = (a+b)+c =21+15=36.
-
Автор:
kit-katcdls - 6 лет назад
-
0
-
-
Треугольник ABC, угол A равен α; радиусы вписанной и описанной окружности r и R. Как обычно, напротив угла лежит одноименная сторона, только обозначенная маленькой букой (то есть BC = a; AB = c; AC = B);Пусть стороны касаются вписанной окружности в точках M (BC), N (AC), K (AB). Я обозначаю x = AK = AN; y = BK = BM; z = CM = CN;x + y = c;x + z = b;y + z = a;Откуда x - y = b - a; 2*x = c + b - a; x = (c + b - a)/2 = p - a;где p = (a + b + c)/2; ПОЛУпериметр треугольника ABC;Далее все очевидно (O - центр вписанной окружности).Из треугольника AOK;x = r*ctg(α/2); по теореме синусовa = 2*R*sin(α);Откуда p - 2*R*sin(α) = r*ctg(α/2); само собой, периметр равен 2*p;2*p = 4*R*sin(α) + 2*r*ctg(α/2);1) α = 120°; sin(α) = √3/2; ctg(α/2) = 1/√3; R = 3√3; r = √3/2;2*p = 19;2) α = 60°; sin(α) = √3/2; ctg(α/2) = √3; R = 5√3; r = √3;2*p = 36;
-
Автор:
raúlwwmi - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
- Что такое урочные лета??
-
Помогите пожалуйста
0,5 моль метанола при нагревании с бромоводородом дали 38 г бромметана.Определить выход бромметана в процентах. -
Для испарения воды, находящейся при температуре 100 град, понадобилось 1610 кДж теплоты. Чему равна масса испарившейся воды?
-
Предмет:
Физика -
Автор:
nataliavazquez - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
что такое бозон Хиггса
How much to ban the user?
1 hour
1 day
100 years
