-
Для кого-то, это легкая задача !
Найдите объем призмы, в основаниях которой лежат правильные шестиугольники со сторонами 2, а боковые ребра равны 2 корней из 3 и наклонены к плоскости основания под углом 30.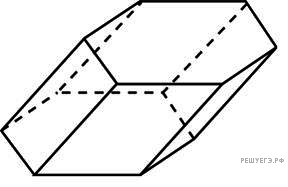
-
Предмет:
Геометрия -
Автор:
matildadougherty - 6 лет назад
-
Ответы 1
-
Найдите объем призмы, в основаниях которой лежат правильные шестиугольники со сторонами 2, а боковые ребра равны 2√3 и наклонены к плоскости основания под углом 30º.Объем призмы находят произведением площади её основания на высоту. Основание данной призмы - правильный шестиугольник, который состоит из 6 правильных треугольников со стороной, равной 2.Площадь правильного треугольника S=(а²√3):4S=4√3):4=√3 (ед.площади)Площадь основания равна в 6 раз больше:S (o)=6*√3 (ед.площади)Чтобы найти высоту призмы, опустим из вершины А₁ верхнего основания перпендикуляр А1Н на плоскость, содержащую нижнее основание, и соединим Н с вершиной А нижнего основания.Треугольник АНА₁ - прямоугольный. Так как угол НАА₁=30º, то А₁Н=АА1:2=√3V призмы=S*H=6*√3*√3=18 (ед. объема)

-
Автор:
ameliab1e9 - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
В царствование Александра 2 произошло:
а) реформа государственных крестьян
б) земская реформа
в) восстание декабристов-
Предмет:
История -
Автор:
armando5ikt - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Определите формулу общего элемента последовательности по ее первым элементам:
{-3; 5; -7; 9;…}-
Предмет:
Математика -
Автор:
gay44 - 6 лет назад
-
Ответов:
4 -
Смотреть
-
-
Как называется тип рынка, в котором продажу товара осуществляет один продавец?
а) олигополия
б) монополия
в) монопсония -
Решите ребус! В букве Й написано 8 раз ТИ
-
Предмет:
Русский язык -
Автор:
babe1swc - 6 лет назад
-
Ответов:
5 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
