Задать вопрос Регистрация
Помочь другим

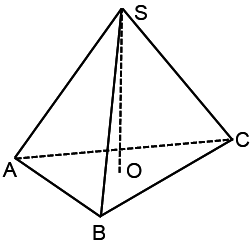
  • Дана правильная треугольная пирамида,боковое ребро которой равно 14,а сторона основания 9.Нужно найти высоту пирамиды.

    question img

Ответы 1

  • так как пирамида правильная, то в основании лежит равносторонний треугольник, найдем его площадь по формуле: S= \frac{ a^{2} \sqrt{3} }{4} S= \frac{81 \sqrt{3} }{4} с другой стороны площадь этого же треугольника найдем: S=1/2*CH*ABCH - высота и медиана \frac{81 \sqrt{3} }{4} = \frac{9}{2} *CHCH= \frac{9 \sqrt{3} }{2} CO:OH=2:1 (по свойству медиан)CO=3√3SOC - прямоугольныйпо теореме ПифагораSO= \sqrt{14^2-(3 \sqrt{3} )^2}=13 Ответ: 13  

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years