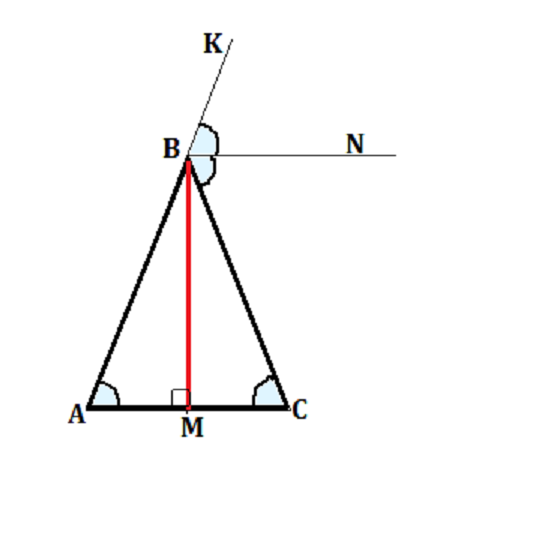
Биссектриса BN внешнего угла при вершине B треугольника ABC параллельна стороне AC. Определите угол MBN, который биссектриса BN образует с медианой BM данного треугольника.

Дан треугольник АВС. ВN || AC Угол КВС- внешний при вершине В.  ∠ KBN= ∠NBC по условию (BN - биссектриса)      ∠ KBN=∠ BAC как соответственные при параллельных прямых BN   и АС и секущей КА     ∠NBC=∠ВCA как накрестлежащие. ⇒ ∠ВАМ= ∠ВСМ и Δ АВС - равнобедренный. ⇒ВМ - медиана и высота равнобедренного треугольника АВС. ⇒∠ВМС=90ºТ.к. BN || АС,  угол МВN= углу ВМС=90º