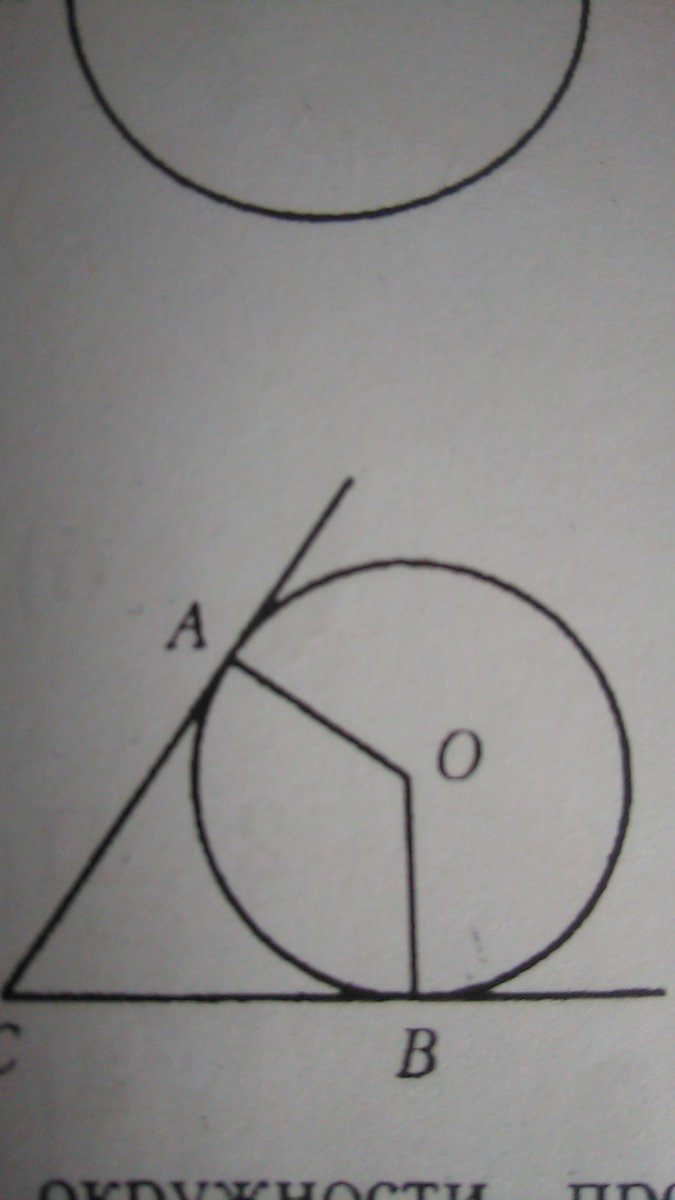
Хорда AB стягивает дугу окружности в 75°.Касательные к окружности,проведённае в точках A и B, пересекаются в точке O.Найдите AOB. Ответ дайте в градусах.

Если касательные пересекаются в точке О, тогда центр окружности обозначим точкой О₁ Касательные АО и ВО, радиусы окружности АО₁ и ВО₁ образовали четырёхугольник АО₁ВО, у которого<О₁АО = <О₁ВО = 90° (касательные в точке касания всегда перпендикулярны радиусу, проведённому к точке касания).Хорда АВ стягивает дугу АВ, равную 75°, значит  центральный угол, который опирается на эту хорду, < АО₁В = 75°Сумма углов выпуклого четырёхугольника всегда равна 360°. Величины трёх углов знаем, теперь найдём искомый <АОВ<АОВ = 360° - (<АО₁В + <ОАО₁ + <ОВО₁)<АОВ = 360° - (75° + 90° + 90°) = 360° - 255° = 105°Ответ: <АОВ = 105°