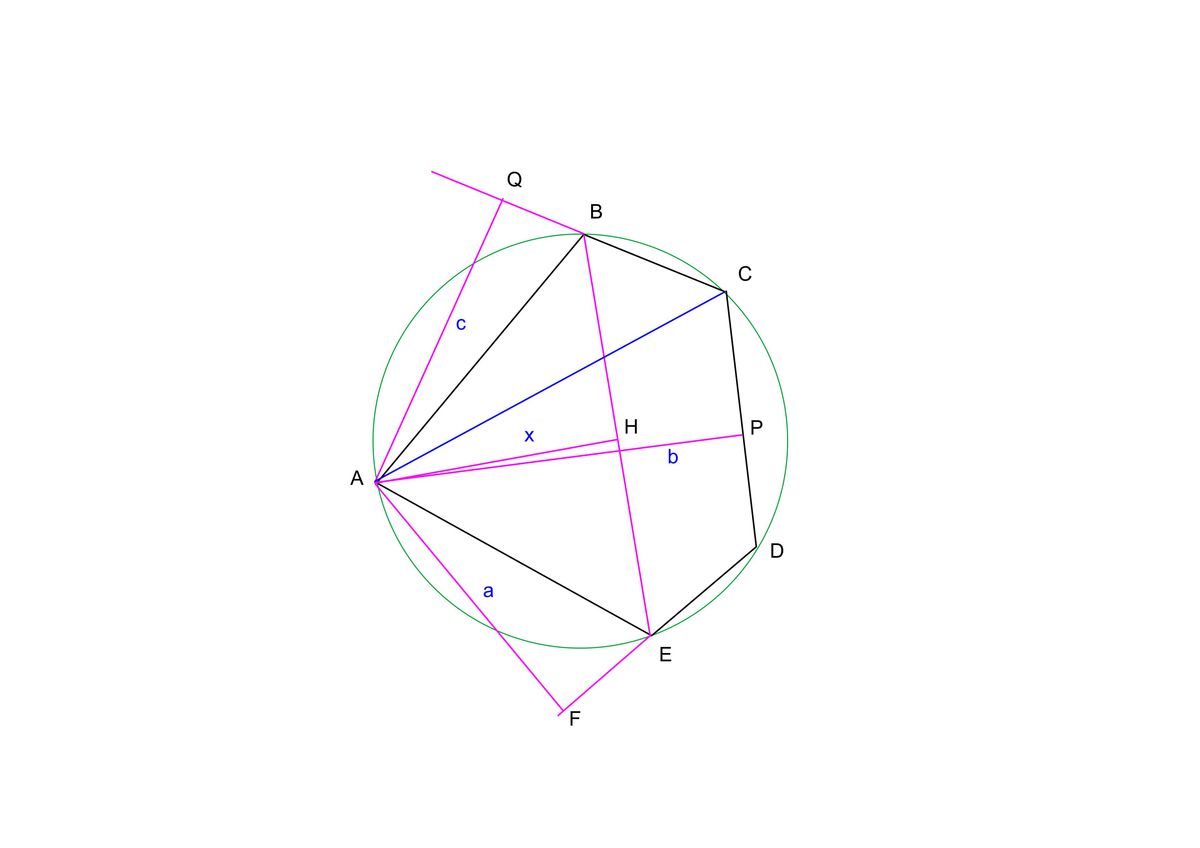
18. Пятиугольник ABCDE вписан в окружность. Из вершины А опущены перпендикуляры AF, AH, AP и AQ на прямые DE, BE, CD и ВС соответственно. а) Докажите, что угол FAH равен углу PAQ. б) Найдите АН, если AF = a, AP = b, AQ = c.

а) Поскольку четырехугольники AHEF и AQCP имеют (каждый) по 2 прямых угла, а четырехугольник BCDE - вписанный, то∠FAH = 180° - ∠FEH = ∠BED = 180° - ∠BCD = ∠PAQ;б) ∠QCA = ∠HEA; это вписанные углы, опирающиеся на дугу AB; поэтому прямоугольные треугольники QCA и AHE подобны.∠AEF = ∠ACP; так как оба они в сумме с углом AED дают 180°.поэтому подобны прямоугольные треугольники AFE и ACP.Отсюда легко составить пропорцииc/AC = x/AE; (x = AH);b/AC = a/AE;если одно разделить на другое, получитсяc/b = x/a;x = ac/b;