-
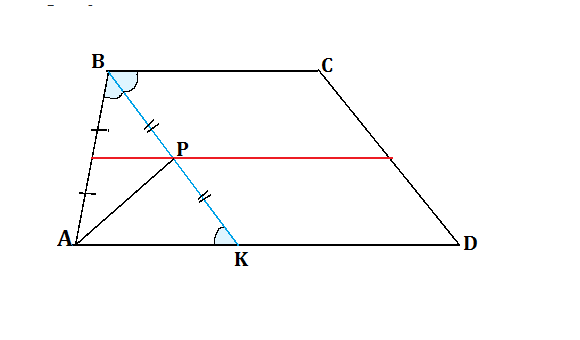
У трапеції ABCD (AD II BC) бісектриса кута ABC перетинає середню лінію в точці P. Доведіть, що кут APB = 90 градусів.
-
Предмет:
Геометрия -
Автор:
bitsypatterson - 6 лет назад
-
Ответы 1
-
В трапеции ABCD (AD II BC) биссектриса угла ABC пересекает среднюю линию в точке P. Докажите, что угол APB = 90 градусов. --Биссектриса делит угол АВС пополам. Пусть она пересекает АД в точке К. Угол СВК равен углу ВКА как накрестлежащий. Но СВК=АВК по условию ⇒ углы пи ВК равны, и треугольник ВАК - равнобедренный. Средняя линия трапеции является и средней линией треугольника АВК и делит стороны пополам. ВР=РК.⇒ АР - медиана треугольника ВАК. Так как в равнобедренном треугольнике медиана является и биссектрисой, и высотой, АР - выстоа, перпендикулярна ВК и угол АРВ=90º
-
Автор:
jimmykcmh - 2 года назад
-
18
-
-
Добавить свой ответ
Еще вопросы
-
чему равна площадь прямоугольника если его ширина равна 12 см. что составляет 3/4длины?
-
Предмет:
Математика -
Автор:
doctor76 - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Папа и сын плывут на лодке против течения. В какой-то момент сын уронил за борт папину шляпу. Только через 20 минут папа заметил пропажу, быстро развернул лодку, и они поплыли вниз по течению с той же собственной скоростью. За сколько минут они догонят шляпу?
-
Предмет:
Математика -
Автор:
marcel - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
В столовую привезли 825 кг крупы. Риса и гречневой крупы 604 кг а гречневой и пшёной 528 кг. Сколько килограмов каждой крупы завезли в столовую?
-
Предмет:
Математика -
Автор:
ifigenia - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Приведите пример квадратичной функции,которая принимает значения,не превосходящие -2.
-
Предмет:
Математика -
Автор:
scrappy - 6 лет назад
-
Ответов:
0 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
