-
Пожалуйста помогите с задачой ?
Зная координаты вершин треугольника в пространстве, определите отношение площади вписанной в него окружности к площади описанной окружности вокруг этого же треугольника.
нам известны x1 , y1 , z1 , x2 , y2 , z2 , x3 , y3 , z3
пример 0 0 0 0 0 1 0 1 0 ответ 0.172
формулу или решение покажите ?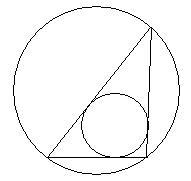
-
Предмет:
Геометрия -
Автор:
mouseroach - 6 лет назад
-
Ответы 1
-
Стороны треугольника находим по формуле: d =√((х2 - х1 )² + (у2 - у1 )² + (z2 – z1 )²).Получаем длины: 1, √2 и 1.Зная стороны, находим радиусы:- вписанной окружности r = √((p-a)(p-b)(p-c)/p). a b c p 2p 1 1.4142136 1 1.7071068 3.414213562 r = 0.2928932 Sr = 0.269506.- описанной окружности R = abc / (4√(p(p-a)(p-b)(p-c)). a b c p 2p 1 1.4142136 1 1.7071068 3.414213562 R = 0.707106781 S = 1.570796 Sr /S = 0.171573Можно добавить, что треугольник прямоугольный с острыми углами по 45 градусов.
-
Автор:
paris - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
- (x-4b)(x^2+4Xb+16b^2)+64b^3+x^3+b^2 при x=1 b=-2 пожалуууйста решите!!!
-
Подскажите, пожалуйста, главную мысль рассказа Толстого "Корова"
-
Предмет:
Литература -
Автор:
edgar40 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
запиши следующие числа 101 112 131
-
Предмет:
Математика -
Автор:
beckham - 6 лет назад
-
Ответов:
3 -
Смотреть
-
-
(ab^-1+a^-1*b+1)(a^-1-b^-1)^2/ a^2b^-2+a^-2b^2-(ab^-1+a^-1b) - 1-a^2/ab
-
Предмет:
Алгебра -
Автор:
frau fraulgkt - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
