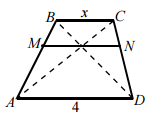
Отрезок MN параллелен основаниям АD и ВС трапеции АВСD и проходит через точку пересечения диагоналей. Известно что MN = 1,6 и АD = 4. Найти меньшее основание трапеции и расстояние между серединами диагоналей.

При решения задачи применим  свойство трапеции, выведенное из подобия треугольников, образованных ее основаниями и диагоналями ( при желании  доказательство можете найти в сети):Отрезок, параллельный основаниям трапеции, проходящий через точку пересечения диагоналей и соединяющий две точки на боковых сторонах, делится точкой пересечения диагоналей пополам. Его длина есть среднее гармоническое оснований трапеции. МN = 2ab/(a + b), где а- меньшее основание, b- большее. ВС обозначим= а1,6=2 а*4: (а+4) 1,6*(а+4)=8а 6,4=8а-1,6а а=6,4:6,4=1 ВС=1 Другое свойство трапеции: Отрезок, соединяющий середины диагоналей трапеции, равен полуразности оснований. КЕ=(АД-ВС):2КЕ=(4-1):2=1,5