Периметр треугольника АВС равен 9 радиус вписанной в этот треугольник окружности равен √3.Найти расстояние от центра вписанной окружности до вершины В, если длина стороны АС равна 3,5.

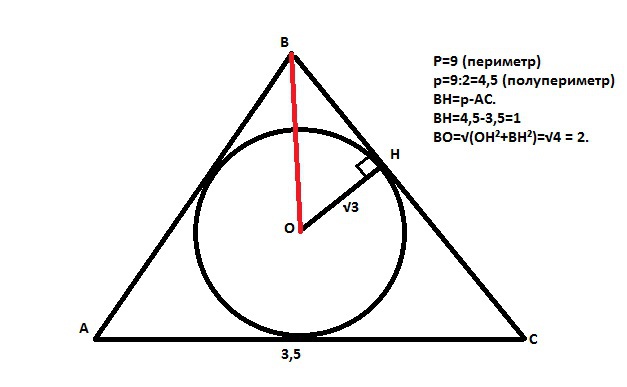
Пусть в треугольнике АВС точка О - центр вписанной окружности. Тогда перпендикуляр ОН в точку касания этой окружности со стороной треугольника ВС - это радиус вписанной окружности. Есть свойство: "Расстояние от вершины В треугольника до точки, в которой вписанная окружность касается стороны, равно  р-b, где р - полупериметр, а b - сторона напротив вершины В".  Тогда в нашем случае полупериметр =9:2=4,5 и ВН=4,5-3,5=1. По Пифагору найдем расстояние от центра до вершины В: ВО=√(ВН²+ОН²)=2.Ответ:расстояние от центра до вершины В равно 2.