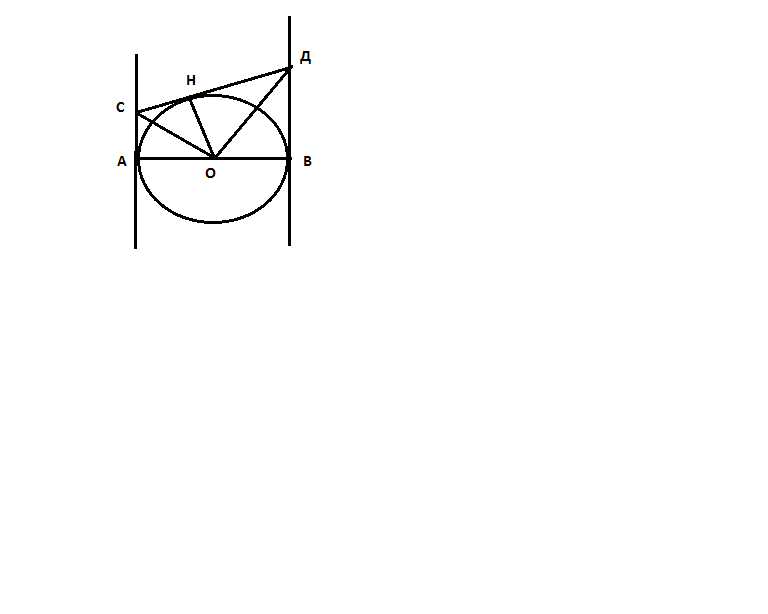
АВ - диаметр круга. через точки А и В проведены две касательные к окружности. третья касательная пересекает первые две в точках С и Д. докажите что квадрат радиуса круга равна произведению отрезков СА и ДВ

Круг с центром О, диаметр АВ=2ОА=2RТретья касательная касается круга в точке Н.Т.к. отрезки касательных к окружности, проведенных из одной точки, равны, то СА=СН и ДВ=ДНПолучается, что круг вписан в ∠АСД и в ∠СДВ, а если окружность вписана в угол, то ее центр лежит на биссектрисе этого угла, т.е. СO - биссектриса ∠АСД.и ДО - биссектриса ∠СДВ.Также СO - биссектриса ∠АОН и ДО - биссектриса ∠ВОН.∠АОН и ∠ВОН - смежные, значит СО⊥ДОВ прямоугольном ΔСОД ОН- высота, проведенная из прямого угла к гипотенузе СД (касательная к окружности перпендикулярна к радиусу, проведенному в точку касания), значит ОН²=СН*ДН=СА*ДВ, ч.т.д