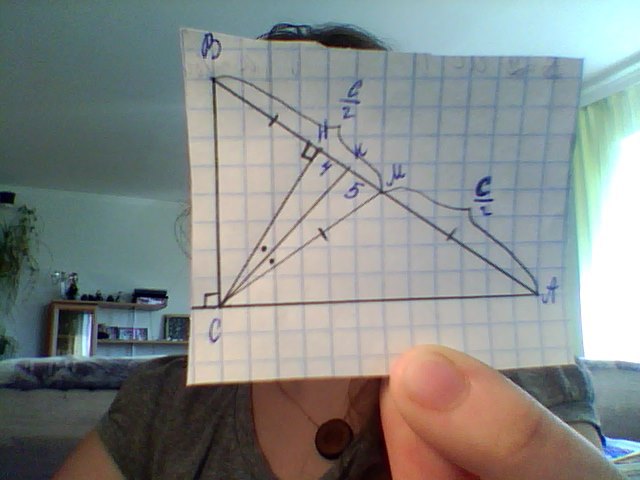
В прямоугольном треугольнике ABC (угол C - прямой) биссектриса CK делит пополам угол между медианой CM и высотой CH. Найдите стороны треугольника , если HK=4, KM=5

Спасибо большое очень хорошее решение)

По свойству биссектрисы СН/НК=СМ/КМСН=4СМ/5=0,8СМТ.к. СМ - медиана из прямого угла, то СМ=ВМ=МАВМ=ВН+НК+КМ=ВН+9ВН=ВМ-9=СМ-9НА=НК+КМ+МА=9+СМТ.к. СН - высота из прямого угла, то СН²=ВН*НА=(СМ-9)(СМ+9)=СМ²-81Подставим(0,8СМ)²=СМ²-810,36СМ²=81СМ=√81/0,36=√225=15Значит гипотенуза АВ=2*15=30СН=0,8*15=12ВН=15-9=6Катет ВС=√ВН²+СН²=√36+144=√180=6√5Катет АС=√АВ²-ВС²=√900-180=√720=12√5Ответ: 6√5; 12√5; 30