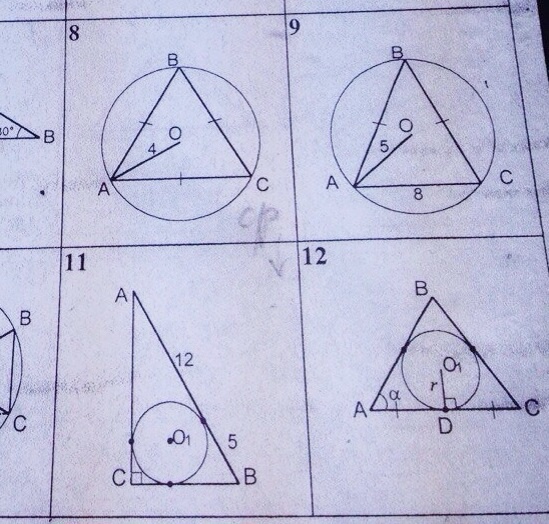
О-центр окружности ,описанной около ΔАВС О1-центр окружности вписанной в ΔАВС найдите площадь Δ АВС ,помогите пожалуйста решить 9,11

Спасибо

9) Проведем высоту  BH, она одновременно является и медианой AD=CD=AC/2=4  т.е. BH серединный перпендикуляр стороны (отрезка) AC.Центр описанной окружности O лежит на BH.Из  ΔAOD : DO =√(AO² -AD²) = √(R² -(AC/2)²) =√(5² -4²)=√3² =3.S =AC*BH/2 =AC*(DO +OB)/2 =AC*(DO +R)/2 =8(3+5)/2 =32 кв.ед.ответ :  32 кв.ед. ----------------------------11) Через D,E и F обозначаем точки касания соответственно сторон CB ,CA и AB с окружностью вписанной в треугольник.S =AC*CB/2 =(AE+EC)*(BD+DC)/2 =(AF+r)*(BF+r)/2 =AF*BF +(AF+BF)r+r²)/2.S =AF*BF +(AF+BF)r+r²)/2    (1)По теореме Пифагора :AB² =AC²+BC² ;(AF+BF)²=(AE+EC)²+(BD+DC)² ;(AF+BF)²=(AF+EC)²+(BF+DC)² ;(AF+BF)²=(AF+r)²+(BF+r)² ;AF²+2AF*BF+BF² =AF² +2AF*r+r² +BF²+2BF²*r+r² ;AF*BF =AF*r +BF*r+r² ;AF*BF =(AF +BF)*r+r² ;Полученное значение   (AF +BF)*r+r² поставим  в (1)   получим :S = AF*BF. S =12*5 =60 кв.ед.ответ :  60 кв.ед..