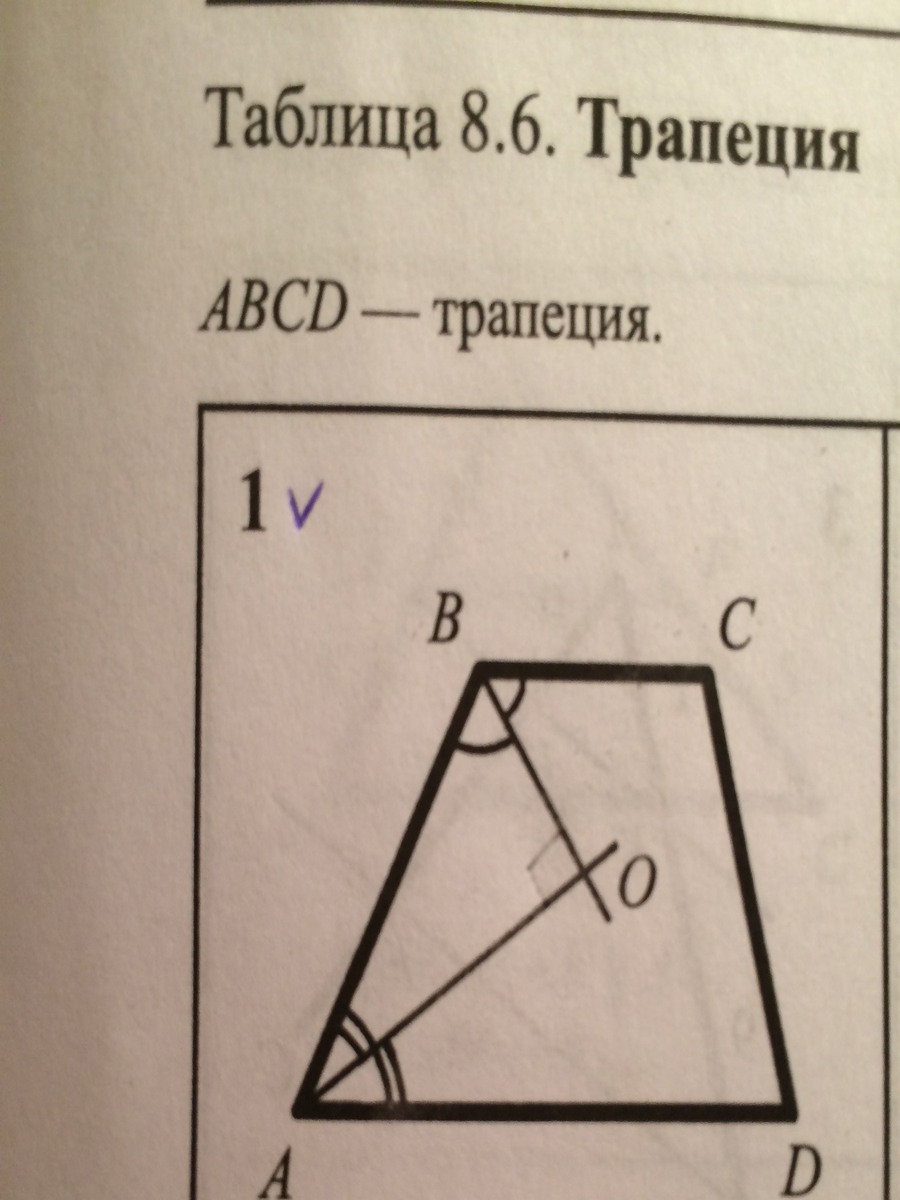
Дано: ABCD-трапеция. Доказать угол АОВ = 90

Не всегда более короткое решение приходит в голову сразу). Есть и третье решение. Т.к. треугольник АВЕ - равнобедренный из равенства углов 1 и 5. а АО - биссектриса, то АО и высота, перпендикулярная ВЕ.

Я вижу такое решение... Если мы продолжим BO до пересечения AD (см. приложение), то получим угол BEA, который равен углу СBO - как накрест лежащий угол при параллельных прямых AD и BC. Мы знаем, что ∠AOB=180-(∠1+∠3). Но в треугольнике AOE: ∠5=∠1, а ∠4=∠3, значит, ∠AOE= 180-(∠5+∠4) = 180-(∠1+∠3) = ∠AOB. Но, ∠AOE и ∠AOB - смежные, значит, они оба равны 90°. P.S. Возможно, есть более рациональное доказательство...

Сумма углов трапеции, прилегающих к боковой стороне (<А и <В), равна 180°. Следовательно, сумма их половин( АО и ВО - биссектрисы) равна 90°. Отсюда угол АОВ=90° (по теореме о сумме углов треугольника 180°-90°=90°.)Что и требовалось доказать.