-
Нужно найти площадь треугольника ABC во всех случаях, кроме 12 задания.
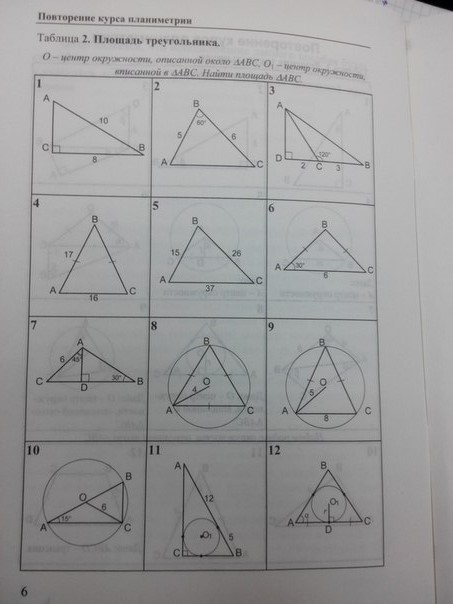
-
Предмет:
Геометрия -
Автор:
damarionmeadows - 6 лет назад
-
Ответы 1
-
1) AC = √(AB^2 - BC^2) = √(10^2 - 8^2) = 6S = AC*BC/2 = 6*8/2 = 242) S = 1/2*AB*BC*sin ∠ABC = 1/2*5*8*sin 60° = 20*√3/2 = 10√33) ∠DCA = 180° - ∠BCA = 180° - 120° = 60°AD = CD*tg ∠DCA = 2*tg 60° = 2√3S = AD*DB/2 = 2√3*5/2 = 5√34) BC = AB = 17p = (AB + BC + AC)/2 = (17 + 17 + 16)/2 = 25S = √[p(p-AB)(p-BC)(p-AC)] = √[25*(25-17)(25-17)(25-16)] = √(25*8*8*9) = 1205) p = (AB + BC + AC)/2 = (15 + 26 + 37)/2 = 39S = √[p(p-AB)(p-BC)(p-AC)] = √[39*(39-15)(39-26)(39-37)] = √(39*24*13*2) = = √(3*13*4*6*13*2) = 13*2*6 = 1566) AB = BC = AC/(2cos ∠CAB) = 6/(2cos 30°) = 6/(2√3/2) = 6√3/3 = 2√3∠ABC = 180° - ∠CAB - ∠CBA = 180° - 30° - 30° = 120°S = 1/2*AB*BC*sin ∠ABC = 1/2*2√3*2√3*sin 120° = 6√3/2 = 3√37) AD = CD = 6/√2 = 3√2BD = AD/tg ∠ABD = AD/tg 30° = 3√2 / (1/√3) = 3√2*√3 = 3√6S = BC*AD/2 = (3√2 + 3√6)*3√2/2 = 3√2*3√2/2 + 3√6*3√2/2 = 9 + 9√38) AB = BC = AC = OA*√3 = 4√3S = AB^2*√3/4 = 16*3*√3/4 = 12√39) Проведем в треугольнике высоту BHOH = √(OA^2 - AH^2) = √(5^2 - 4^2) = 3BO = OA = 5BH = BO + OH = 5 + 3 = 8S = AC*BH/2 = 8*8/2 = 3210) OA = OB = OC = 6; AB = OA + OB = 12AC = AB*cos 15 = 12*√(2 + √3)/2 = 6√(2 + √3)BC*sin 15 = 12*√(2 - √3)/2 = 6√(2 - √3)S = AC*BC/2 = 6√(2 + √3)*6√(2 - √3) = 36*√(4 - 3) = 3611) По одной гипотенузе я не могу найти площадь треугольника.Если это треугольник (8, 15, 17) - единственный целочисленный треугольник с гипотенузой 17, то его площадьS = AC*CB/2 = 15*8/2 = 60
-
Автор:
allisson - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
СРОЧНО сообщение о книге Алиса в стране чудес
-
Предмет:
Литература -
Автор:
dinosaurhrqj - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Решите ребус:________________________.
Ребят срочно надо.-
Предмет:
Литература -
Автор:
lena14 - 6 лет назад
-
Ответов:
4 -
Смотреть
-
-
Мне задали подобрать редкие,красивые эпитеты к картине "Летом",а я не знаю какие мне подобрать. Помогите!
-
Предмет:
Русский язык -
Автор:
lópezsvkk - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Составте 5 предложения из этих слов .Огород,овощи,огурец,картофель,морковь,капуста,горох,урожай.
-
Предмет:
Русский язык -
Автор:
yusufmcconnell - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
