-
Дан куб ABCDA1B1C1D1 с ребром равным а. Дан куб ABCDA1B1C1D1 с ребром равным а. Точка К принадлежит ребру АА1, точка L -ребру DD1. При этом A1K :
КА=1:3, D1L : LD=2:1. Проведена прямая KL.Используя рисунок Найдите длину С1L,KL,EF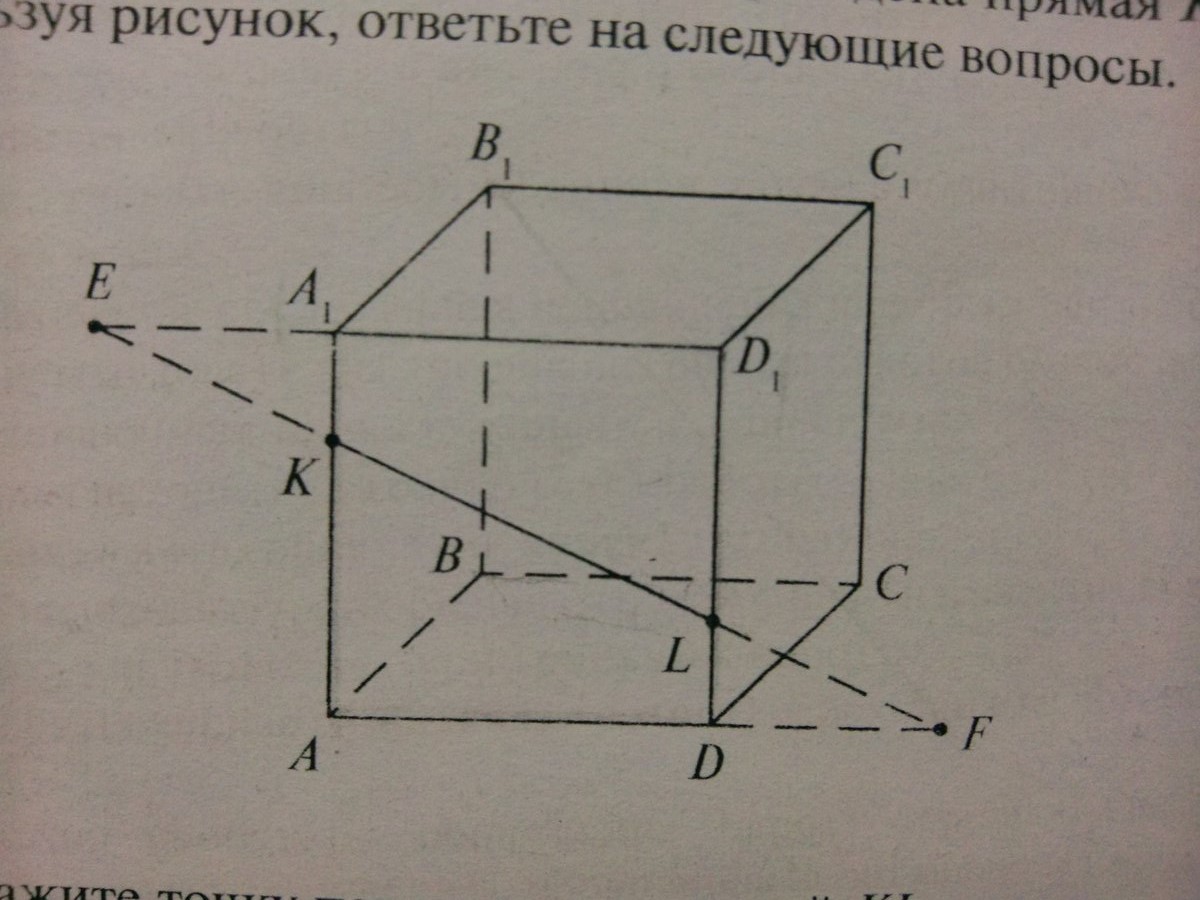
-
Предмет:
Геометрия -
Автор:
jaidencervantes - 6 лет назад
-
Ответы 1
-
Так как А₁К : КА = 1 : 3, то А₁К - одна часть, КА - 3 таких части, а АА₁ - 4 части. Значит,
А₁К = а/4, КА = 3а/4.
Так как D₁L: LD = 2 : 1, то LD - одна часть, D₁L - две таких части, а DD₁ - 3 части.
Т.е. D₁L = 2a/3, LD = a/3.
ΔС₁D₁L: по теореме Пифагора
С₁L = √(C₁D₁² + D₁L²) = √(a² + (2a/3)²) = √(a² + 4a²/9) = a√13/3
Проведем КК₁║A₁D₁. КК₁ = A₁D₁ = a.
К₁L = D₁L - D₁K = D₁L - A₁K = 2a/3 - a/4 = 5a/12
ΔKK₁L: по теореме Пифагора
KL = √(KK₁² + K₁L²) = √(a² + 25a²/144) = √(169a²/144) = 13a/12
ΔEA₁K подобен ΔED₁L по двум углам (прямоугольные, угол при вершине Е общий):
EK : EL = A₁K : D₁L
EK : (EK + KL) = (a/4) : (2a/3) = 3 : 8
8EK = 3(EK + KL)
8EK = 3EK + 13a/12
5EK = 13a/12
EK = 13a/60
ΔFDL подобен ΔFAK по двум углам (прямоугольные, угол при вершине F общий):
FL : FK = LD : AK
FL : (FL + KL) = (a/3) : (3a/4) = 4 : 9
9FL = 4(FL + KL)
9FL = 4FL + 4KL
5FL = 13a/3
FL = 13a/15
EF = EK + KL + FL
EF = 13a/60 + 13a/12 + 13a/15 = 13a(1/60 + 5/60 + 4/60) = 13a · 1/6 = 13a/6

-
Автор:
adrián58 - 6 лет назад
-
0
-
-
Добавить свой ответ
- 3 географических объектов названных в честь российских землепроходцев
-
Что входит в структуру семейного бюджета
-
Предмет:
Другие предметы -
Автор:
andre862 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
что называется Механическим движением?
-
Предмет:
Физика -
Автор:
averywillis - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
как звали спицына из романа дубровский
-
Предмет:
Литература -
Автор:
mara - 6 лет назад
-
Ответов:
0 -
Смотреть
-
