Одна из сторон треугольника разделена на три равные части ,и через точки деления проведены прямые,параллельные другой стороне.Найдите отношения площади данного треугольника к площадям треугольников ,отсеченных построенными прямыми.
Если можно с рисунком.
Спасибо.

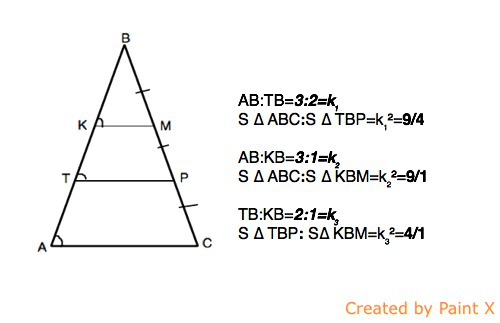
Пусть исходный треугольник будет АВС, а пересекают его прямые КМ и ТР, параллельные АС. КМ ║ТР║ АС⇒ соответственные углы, образованные при их пересечении секущей АВ, равны, а угол В для всех трех треугольников общий. ∆ АВС ~ ∆ТВР~∆ КВМ по двум углам, прилежащим к одной стороне. АВ=3 части, ТВ=2 части. КР=1 часть.       Отношение площадей подобных фигур равно квадрату коэффициента их подобия. АВ:ТВ=3:2=k₁S ∆ ABC:S ∆ TBP=k₁²=9/4AB:KB=3:1=k₂S ∆ ABC:S ∆ KBM=k₂²=9/1TB:KB=2:1=k₃S ∆ ТВР: S∆ КВМ=k₃²=4/1