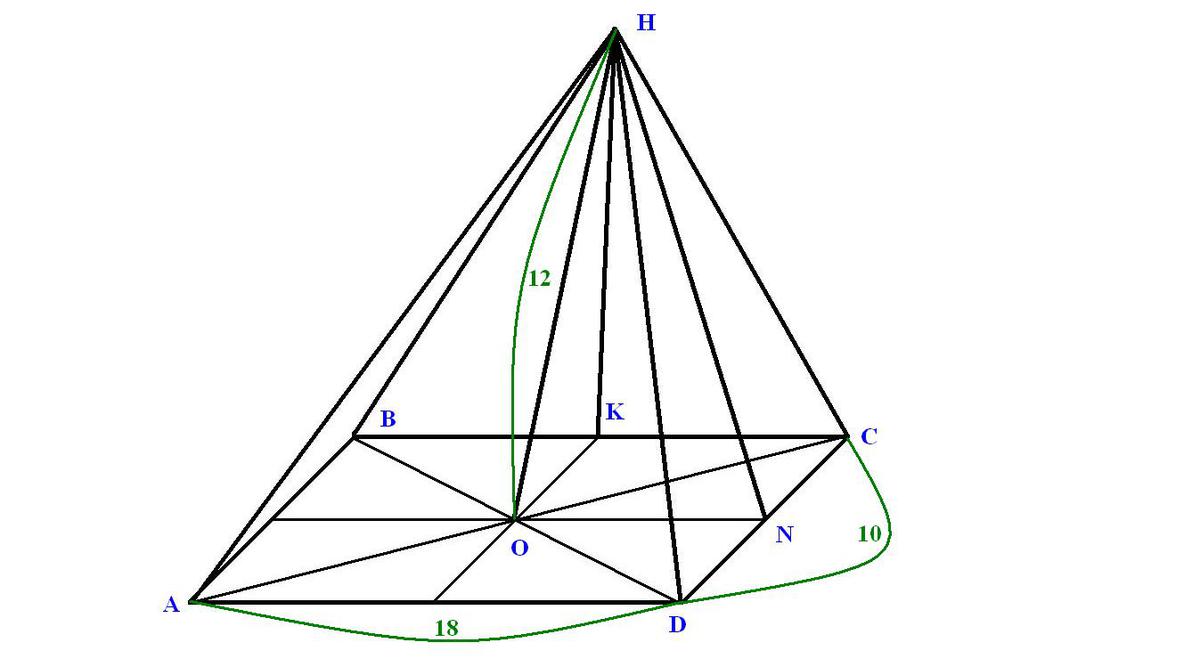
Помогите ПРОШУ!! Основанием пирамиды является прямоугольник со сторонами 18 см и 10 см.Основанием высоты пирамиды,равной 12 см , является точка пересечения диагоналей прямоугольника. 1)Найдите площадь боковой поверхности пирамиды : 2)найдите площадь полной поверхности пирамиды. С рисунком пожалуйста!

Ответы 1

Дано:НABCD - пирамидаABCD - прямоугольникAB=CD=10смAD=ВС=18смНO - высотаНO=12cмS(бок)-?S(полн)-?Решение:S(бок)=S(AНB)+S(BНC)+S(CНD)+S(AНD). Так как треугольники AНB и CНD, а также BНC и AНD попарно равны, то S(бок)=2S(BНC)+2S(CНD).S(BHC)= \frac{1}{2} \cdot BC \cdot HK, где НК - высота, проведенная к стороне ВС. НК можно найти как гипотенузу прямоугольного треугольника НОК, где ОК - половина стороны СD.HK= \sqrt{HO^2+OK^2} =\sqrt{12^2+( \frac{10}{2} )^2} =13(sm).Аналогично, S(CHD)= \frac{1}{2} \cdot CD \cdot HN, где НN - высота, проведенная к стороне СD.HN= \sqrt{HO^2+ON^2} =\sqrt{12^2+( \frac{18}{2} )^2} =15(sm)Получаем:S_{bok}=2S(BHC)+2S(CHD)=2\cdot \frac{1}{2} \cdot BC \cdot HK+2\cdot \frac{1}{2} \cdot CD \cdot HN= \\\ =BC \cdot HK+CD \cdot HN=18\cdot 13+10\cdot 15=384(sm^2)Площадь полной поверхности равна сумме площади боковой поверхности и площади основания:S_{poln}=S_{bok}+S_{osn}=S_{bok}+AD\cdot DC=384+18\cdot10=564(sm^2)Ответ: 384см²; 564см²
- Автор:
  norahvcia
- 2 года назад
- 13
Добавить свой ответ

Еще вопросы

How much to ban the user?

1 hour 1 day 100 years