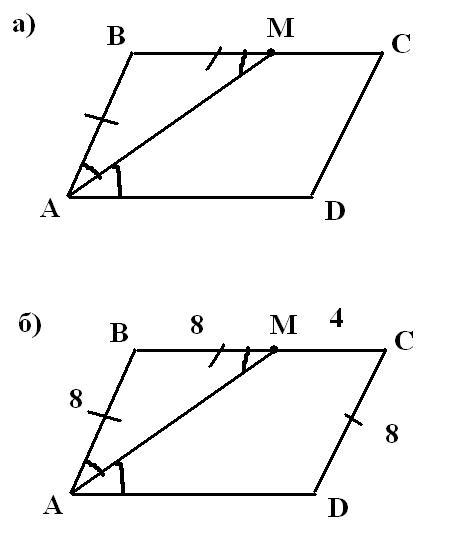
На стороне BC параллелограмма ABCD взята точка M так,что AB = BM.
а)Докажите,что AM - биссектриса угла BAD
б)Найдите периметр параллелограмма,если CD = 8см,CM = 4см Как решить? 8 класс

а) Доказательство:АВ = ВМ, по условию, значит треугольник АВМ - равнобедренный. По свойству равнобедренного треугольника угол ВАМ = углу ВМА.По свойству параллелограмма ВС параллельно АD, АС - секущая, значит угол АМВ = углу МАD, из вышесказанного следует, что угол ВАМ = углу МАD, значит АМ - биссектриссаб) Решение:АВ = СD по свойству параллелограмма,а АВ = ВМ из доказательства. Значит АВ = ВМ = СD = 8 смМС = 4 по условию. ВС = ВМ + МС = 8 + 4 = 12. По свойству параллелограмма ВС = АD = 12теперь можем найти площадь: Р = АВ + ВС + СD + DА = 8 + 12 + 8 + 12 = 40 см