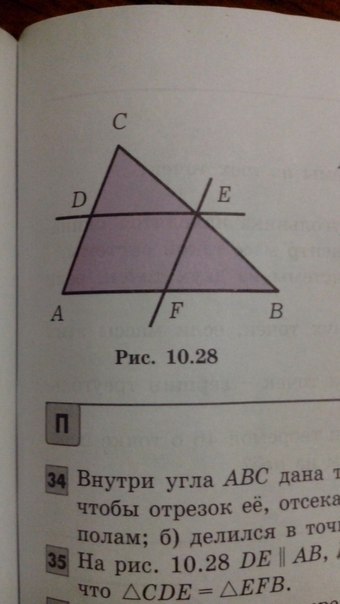
На рис. 10.28 DE ll AB; EF ll AC и D - середина отрезка АС. Докажите, что треугольник CDE = треугольнику EFB. Помогите, пожалуйста, я буду очень рада. Заранее спасибо!

Д - середина АС, ДЕ // АВ => ДЕ - средняя линия тр.АВСа значит Е - середина АС, а т. к. ЕФ // АС = > ЕФ - средняя линия тр. АВСиз того, что ДЕ и ЕФ - средние линии тр. АВС следую равенства:СЕ = ЕВДС = АД = ФЕДЕ = АФ = ФВа из этих равенств следует равенство треугольников СДЕ и ЕФБ (по трем сторонам) что и требовалось доказать 

D - середина АС, DE|| АВ => DE - средняя линия ΔАВС⇒Е - середина BС и ЕF || АС = > ЕF - средняя линия Δ АВС⇒AF=BFСЕ = ЕВDС = АD = FЕDЕ = ВFЗначит ΔСВУ=ΔEFB по трем сторонам/