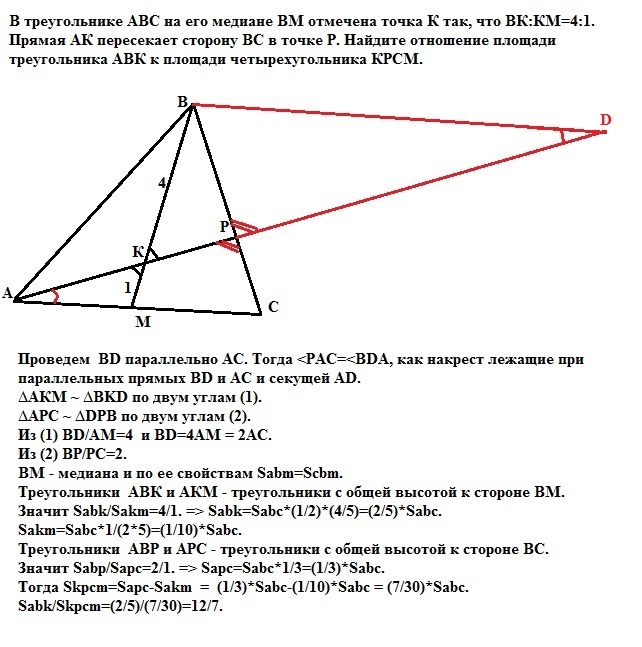
В треугольнике АВС на его медиане ВМ отмечена точка К так, что ВК:КМ=4:1. Прямая АК пересекает сторону ВС в точке Р. Найдите отношение площади треугольника АВК к площади четырехугольника КРСМ.

Для начала найдем отношение ВР/РС. Для этого:Проведем  BD параллельно АС. Тогда <PAC=<BDA, как накрест лежащие при параллельных прямых BD и AC и секущей АD.∆АКМ ~ ∆BKD по двум углам (1).∆АРС ~ ∆DРВ по двум углам (2).Из (1) BD/AM=4  и BD=4AM = 2AC.Из (2) BP/PC=2.ВМ - медиана и по ее свойствам Sabm=Scbm.Треугольники  АВК и АКМ - треугольники с общей высотой к стороне ВМ. Значит Sabk/Sakm=4/1. => Sabk=Sabc*(1/2)*(4/5)=(2/5)*Sabc.Sakm=Sabc*1/(2*5)=(1/10)*Sabc.Треугольники  ABP и APC - треугольники с общей высотой к стороне ВC. Значит Sabp/Sapc=2/1. => Sapc=Sabc*1/3=(1/3)*Sabc.Тогда Skpcm=Sapc-Sakm  =  (1/3)*Sabc-(1/10)*Sabc = (7/30)*Sabc.Sabk/Skpcm=(2/5)/(7/30)=12/7.