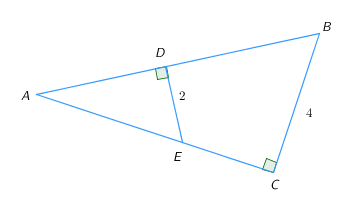
В прямоугольном треугольнике ABC из произвольной точки E катета AC опущен перпендикуляр ED на гипотенузу AB. DE=2, BC=4. Площадь треугольника ADE равна5. Найдите площадь треугольника ABC.

Треугольники ADE и ABC- подобные, ED и BC - сходственные стороны,

сл. - но: ED:BC = 2:4

Sade:Sabc = 2:3

Пусть Sавс - x, тогда:

5:x=2:4

2x=5*4

x=20:2

x=10

 Находим ADисходя из площади и катета DE:

5:2*2=5

Исходя из подобия тр-ков ABC и  EDA

 DE относится к DC как 2/4, т.е. как 1/2

Следовательно AD относится к AC как 1/2

Отсюда находим AC:

5*2=10

Зная катеты тр-ка ABC: АС=10, ВС=4 находим площадь тр-ка

(10*4)/2=40/2=20

             Ответ: S=20