-
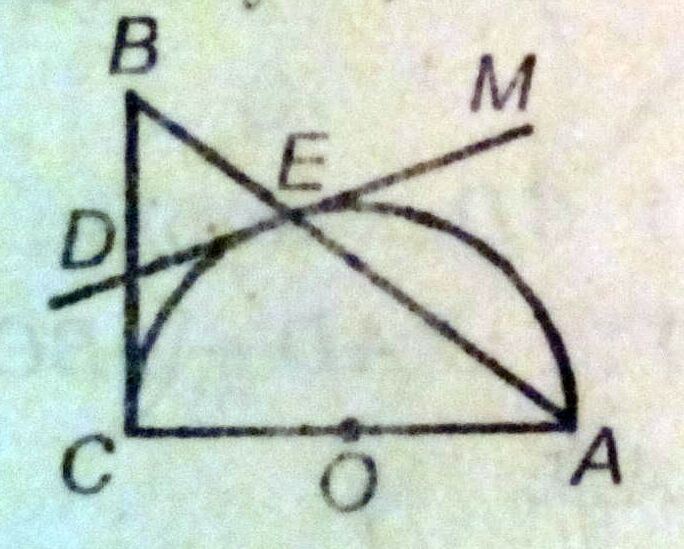
Помогите, пожалуйста, решить задачу. Дано: ABC-прямоугольный треугольник. АС-диаметр, ОА=ОС, ED-касательная. Доказать, что треугольник BDE-равнобедренный.
Ответы 4
-
Спасибо огромное за подробный ответ.
-
Автор:
juliethampton - 6 лет назад
-
0
-
-
Разобрались? Я рада. На картинке легко отметить, а описать гораздо сложнее.
-
Автор:
acejhgd - 6 лет назад
-
0
-
-
Это точно
-
Автор:
willow - 6 лет назад
-
0
-
-
∠ МЕА = половине дуги ЕА - угол между касательной и хордой∠ЕСА= половине дуги ЕА, как вписанный угол, опирающийся на эту дугу∠МЕА=∠ЕСА∠ВЕD=∠МЕА как вертикальные∠ DЕC = половине дуги CЕ - угол между касательной и хордой∠ DCT = половине дуги CЕ - угол между касательной и хордой∠ВАС = половине дуги СЕ, как вписанный угол, опирающийся на эту дугу∠СBA+∠BAC=90° - сумма острых углов прямоугольного треугольника∠ВСЕ+∠ЕСА=90°- по условию угол С - прямойВ этих равенствах ∠ВАС=∠ВСЕЗначит∠СВА=∠ЕСА, а ∠ЕСА=∠МЕА=∠ВЕDИтак∠СВА=∠ВЕDТреугольник ВDE - равнобедренный

-
Автор:
babe79 - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
- Как найти синус 40 градусов?
-
какая граматическая основа в предложении: на Ямале дуют снежные ветра?
-
Предмет:
Русский язык -
Автор:
anabellahester - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Напишите невыдуманную историю про дружбу.
(Задание по искусству)-
Предмет:
Другие предметы -
Автор:
savionlandry - 6 лет назад
-
Ответов:
3 -
Смотреть
-
-
На координатной плоскости задан треугольник АВС. Найдите площадь треугольника, если А (-2; -2), В (-3; 2), С (3; 0).
-
Предмет:
Математика -
Автор:
davis17 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
