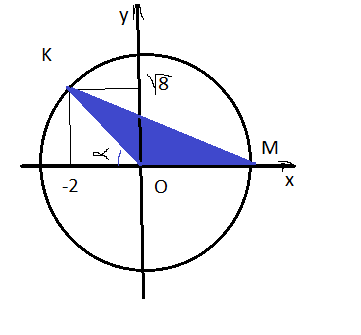
Окружность,заданная уравнением x^2 + y^2=12, пересекает
положительную полуось Ox в точке М , точка K лежит на окружности , её
абцисса равна -2 . найдите площадь треугольника OKM

См. рисунок в приложенииТочка M имеет абсциссу х=√(12) =2√3 ординату у=0   Точка  К имеет асбциссу х=-2   ордината у находится из уравненияу²=12-4у=√8у=2√2точка O (0;0)ОМ имеет длину 2√3ОМ- радиус векторОМ=2√3ОМ=ОК=2√3tg∠КОМ=-√2 ( так как тангенс смежного с ним угла α равен √2    tg α=2√2/2=√2)cos²∠КОМ= 1/(1+tg²∠KOM)=1/3sin²∠КОМ=1-cos²∠KOM=1-(1/3)=2/3sin ∠KOM=√(2/3)S=ОК·ОМ· sin ∠KOM/2= (2√3)²·(√(2/3))/2=2√6 кв. ед