помогите решить задачи на трапецию и среднюю линию

Ответ:

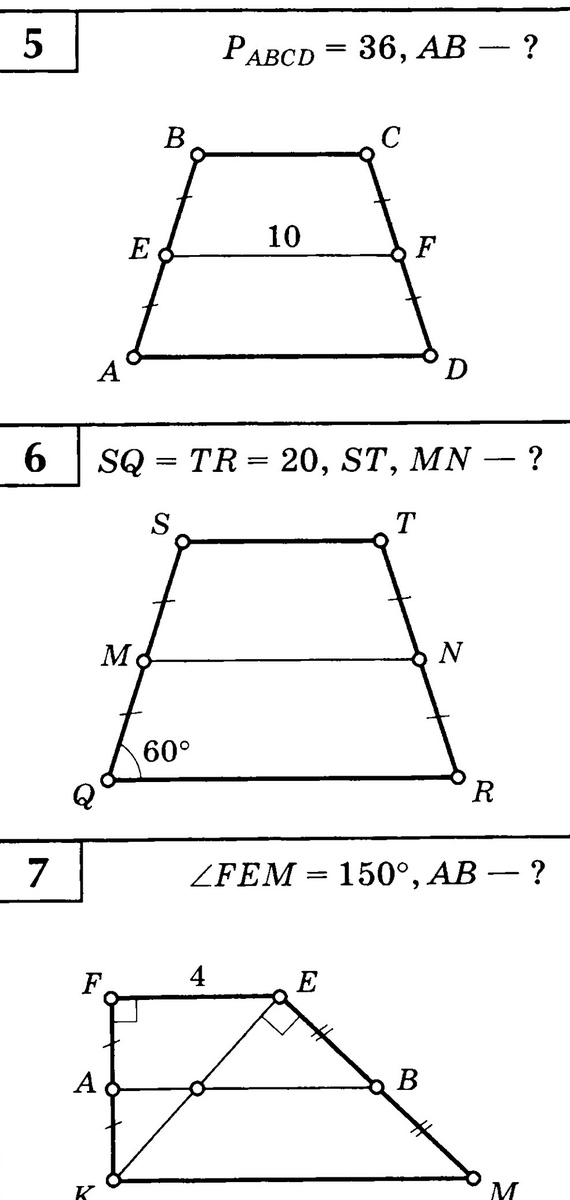
5. AB = 8

6. MN = 20

7. AB = 10

Объяснение:

Средняя линия трапеции параллельна основаниям и равна полусумме оснований.

5.  EF = (AD + BC) / 2 = 10

AD + BC = 10 · 2 = 20

Pabcd = AD + BC + AB + CD = 36

AB + CD = 36 - 20 = 16

AB = CD = 16 /2 = 8

6.  В этой задаче не хватает данных. На рисунке я показала, что эти две трапеции удовлетворяют условию задачи, т.е. однозначно найти длины ST и MN по таким данным невозможно.

Предположим, что длина ST дана. ST = 10. Найти MN.

Проведем SK ║ TR. Тогда STRK параллелограмм (противоположные стороны попарно параллельны). Значит SK = TR = 20.

Треугольник QSK равнобедренный с углом 60° при основании, следовательно, равносторонний.

QK = SQ = 20

МО проходит через середину стороны QS параллельно основанию треугольника, значит МО - средняя линия треугольника QSK.

МО = QK/2 = 10

STNO - параллелограмм (противоположные стороны попарно параллельны), значит ON = ST = 10.

MN = MO + ON =  10 + 10 = 20

7. ∠FEK = ∠FEM - ∠KEM = 150° - 90° = 60°

В прямоугольном треугольнике FEK ∠FKE = 90° - 60° = 30° (сумма острых углов прямоугольного треугольника равна 90°). Значит против этого угла лежит катет, равный половине гипотенузы:

FE = 1/2 KE, ⇒

KE = 2FE = 2 · 4 = 8

Сумма углов трапеции, прилежащих к боковой стороне, равна 180°.

∠EMK = 180° - ∠FEM = 180° - 150° = 30°

В прямоугольном треугольнике EMK ∠ЕКМ = 90° - 60° = 30°.

Тогда против него лежит катет, равный половине гипотенузы:

ЕК = 1/2 КМ, ⇒

КМ = 2ЕК = 2 · 8 = 16

АВ = (FE + KM) / 2 = (4 + 16) / 2 = 20/2 = 10