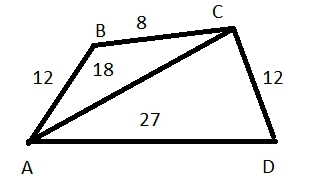
ABCD - трапеция. AB=12 см, BC=8 см, AD=27 см, CD=12 см, AC=18 см. Докажите подобие треугольников ABC и DAC по 2-ому либо 3-ему признаку подобия

кстати, рисунок не правильный, потому что трапеция - это 4х-угольник, у которого 2 стороны параллельны, а 2 другие - нет.Итак,Дано:ABCD - трапеция, AB=12BC=8AD=27CD=12AC=18Доказать: ΔABC и ΔADC подобны.тогда BC II AD, AC - секущая,значит, ∠ACB=∠CAD и ∠CAB=∠ACD - как накрест лежащиеПо второму признаку подобия треугольников (если 2 стороны одного треугольника пропорциональны 2 сторонам другого треугольника, и углы между этими сторонами равны, то треугольники подобны), находим ⇒  ⇒ Стороны AB и BC пропорциональны AC и CD.Все условия подходят под второй признак подобия треугольников.Ответ: ΔABC и ΔADC подобны.