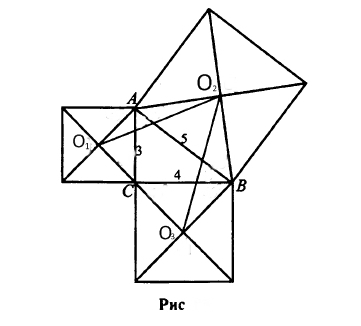
На сторонах треугольника внешним образом построены квадраты. Найдите площадь треугольника, вершинами которого являются центры этих квадратов(О1,02 И О3), если стороны треугольника равны 3, 4 и 5.

Из рисунка (см. вложение) более-менее очевидно, что O2C - биссектриса прямого угла ACB (симметрия налицо). А т.к. углы АСО1, ВСО3 по 45 градусов, то О2С - высота в треугольнике О1О2О3. 

Дальше все ясно, искомая площадь равна 1/2*7/sqrt(2)*7/sqrt(2)=49/4.