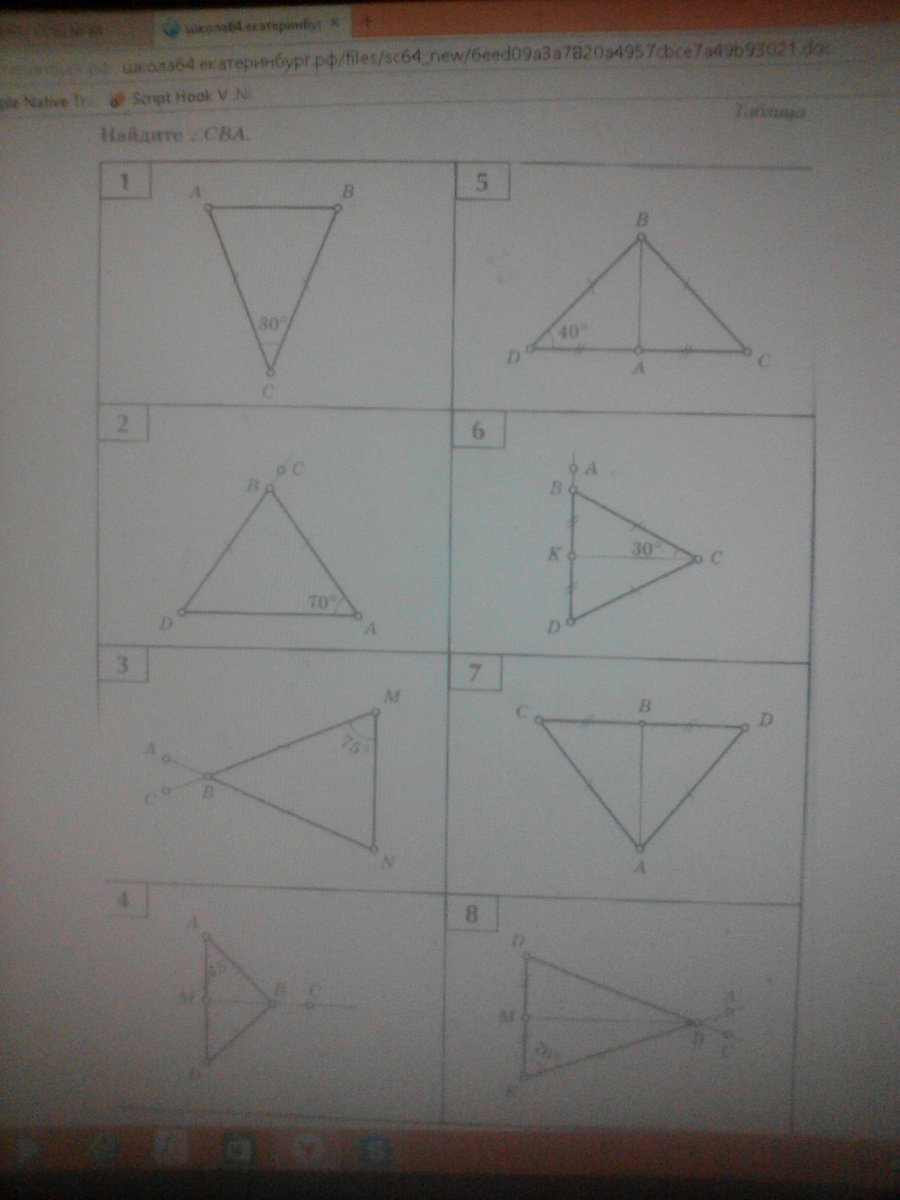
Найдите угол CBA на всех рисунках.Решить с Дано,найти,решение.ПОМОГИТЕ заранее спасибо

1. ΔАВС равнобедренный, значит углы при основании АС равны.∠СВА = ∠САВ = (180° - 30°)/2 = 75°2. ΔABD - равнобедренный, значит углы при основании AD равны. ∠BAD = ∠BDA = 70°.∠СВА - внешний, значит равен сумме двух внутренних, не смежных с ним.∠СВА = ∠BAD + ∠BDA = 140°.3. ΔBMN равнобедренный, значит углы при основании NM равны.∠BMN = ∠BNM = 75°.∠MBN = 180° - (75° + 75°) = 30°∠CBA = ∠MBN = 30° как вертикальные.4. ΔABD равнобедренный, ВМ медиана, проведенная к основанию AD, а значит и высота.∠ВМА = 90°.∠СВА - внешний для треугольника МВА, значит равен сумме двух внутренних, не смежных с ним.∠СВА = ∠ВАМ + ∠ВМА = 45° + 90° = 135°5. ΔDBC равнобедренный, значит углы при основании СD равны. ∠BDС = ∠BСD = 40°. ∠CDB = 180° - (40° + 40°) = 100°ВА - медиана равнобедренного треугольника, значит и биссектриса.∠СВА = ∠CBD/2 = 100°/2 = 50°6. СК - медиана равнобедренного треугольника CBD, проведенная к основанию BD, а значит и высота. ∠СКВ = 90°∠СВА - внешний для треугольника СКВ, значит равен сумме двух внутренних, не смежных с ним.∠СВА = ∠ВКС + ∠ВСК = 30° + 90° = 120°7. ВА - медиана равнобедренного треугольника АСD, проведенная к основанию СD, а значит и высота. ∠СВА = 90°8. ΔЕBD - равнобедренный, значит углы при основании ЕD равны. ∠BЕD = ∠BDЕ = 70°.∠ЕBD = 180° - (70° + 70°) = 40°∠СВА = ∠ЕBD = 40° как вертикальные.