Помогите пожалуйста решить задачу подробно!!!
Даю 57 баллов

Основанием прямоугольного параллелепипеда служит квадрат, диагональ которого равна 12, она составляет угол 30 0 с плоскостью боковой грани. Найдите объём прямоугольного параллелепипеда.

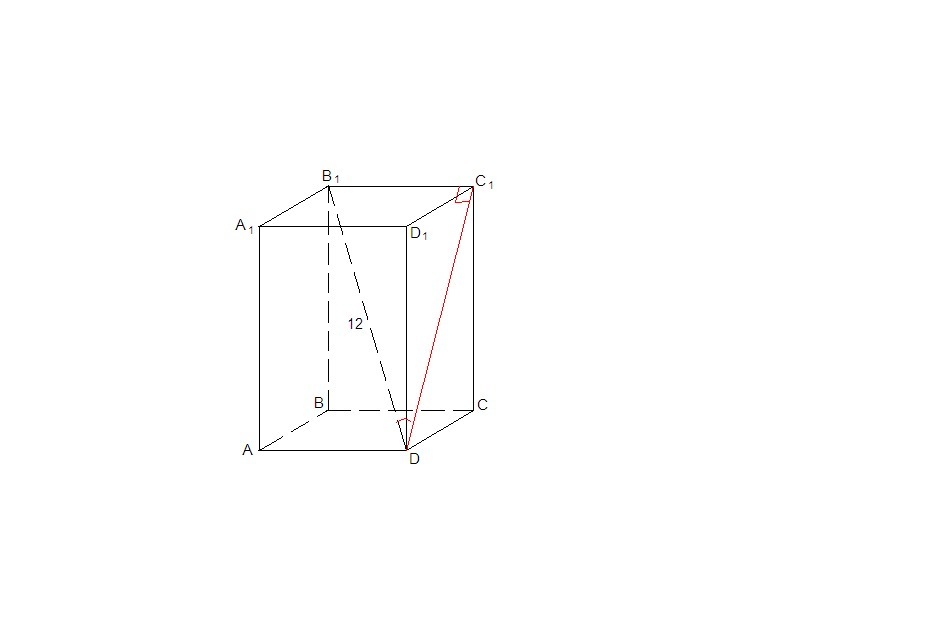
Условие задачи дано с ошибкой: если в основании прямоугольного параллелепипеда квадрат, то диагональ основания составляет с боковой гранью угол 45°, а не 30°. Кроме того, по этим данным невозможно найти высоту прямоугольного параллелепипеда.Задача встречается в таком виде:Основанием прямоугольного параллелепипеда служит квадрат. Диагональ параллелепипеда  равна 12, она составляет угол 30° с плоскостью боковой грани. Найдите объём прямоугольного параллелепипеда.DB₁ - диагональ прямоугольного параллелепипеда.Угол между прямой и плоскостью - угол между прямой и ее проекцией на эту плоскость.В₁С₁⊥(DD₁C₁), значит DC₁ - проекция диагонали DB₁ на плоскость (DD₁C₁), а ∠B₁DC₁ = 30°.ΔB₁C₁D: ∠C₁ = 90°,                  B₁C₁ = DB₁ · sin30° = 12 · 1/2 = 6 - ребро основания                 DC₁ = DB₁ · cos 30° = 12 · √3/2 = 6√3ΔDCC₁: ∠C = 90°, по теореме Пифагора               СС₁ = √(DС₁² - DC²) = √(108 - 36) = √72 = 6√2 - высота параллелепипедаV = Sосн·H = 6² · 6√2 = 216√2