-
Нужна помощь с геометрией. Задачи 3 и 5.
В 3-ей задаче не могу понять, как доказать, что MP-средняя линия трапеции.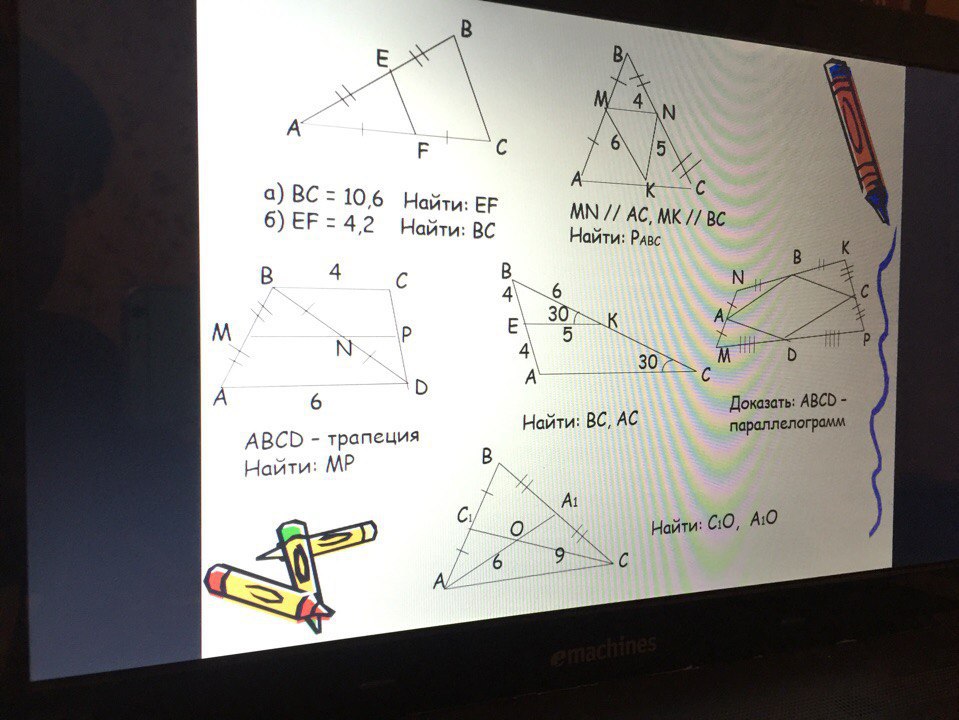
-
Предмет:
Геометрия -
Автор:
ferrera8ii - 6 лет назад
-
Ответы 1
-
3. MN средняя линия треугольника BMN,MN||AD||BC.По теореме Фалеса(Если на одной из двух прямых отложить последовательно равные отрезки и через их концы провести параллельные прямые,пересекающие вторую прямую,то они отсекут на ней равные между собой отрезки) CP=PD,тогда MP-средняя линия трапеции ABCD.MP=1/2(4+6)=55.Проведём прямую MK.В треугольнике MNK AB соединяет середины NC и NK,тогда AB средняя линия этого треугольника,тогда AB||MK,AB=1/2MK. Аналогично и для средней линии DC треугольника KCP. Следовательно,AB=2CK=CD,AB||CK||DC.Если в четырёхугольнике противоположные стороны равны и параллельны,то это--параллелограмм,следовательно,ABCD-параллелограмм.
-
Автор:
hillaryorr - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
начертите какой нибудь прямоугольник, отношение длин сторон которого равно 4:3
Это как?-
Предмет:
Математика -
Автор:
mastera5z2 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
сколько будет (2а)в пятой степени
-
Предмет:
Алгебра -
Автор:
culleno6zz - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
сочинение на тему я слушал дождь
-
Предмет:
Русский язык -
Автор:
brando - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
в битве за Сталинград синтаксический разбор
-
Предмет:
Русский язык -
Автор:
clementinekuvi - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
