AD||CB S(BOC)=36 S(AOD)=16 S(ABCD) = ? О - точка пересечения диагоналей. Надо узнать

AD||CB
S(BOC)=36
S(AOD)=16
S(ABCD) = ?

О - точка пересечения диагоналей.

Надо узнать площадь трапеции.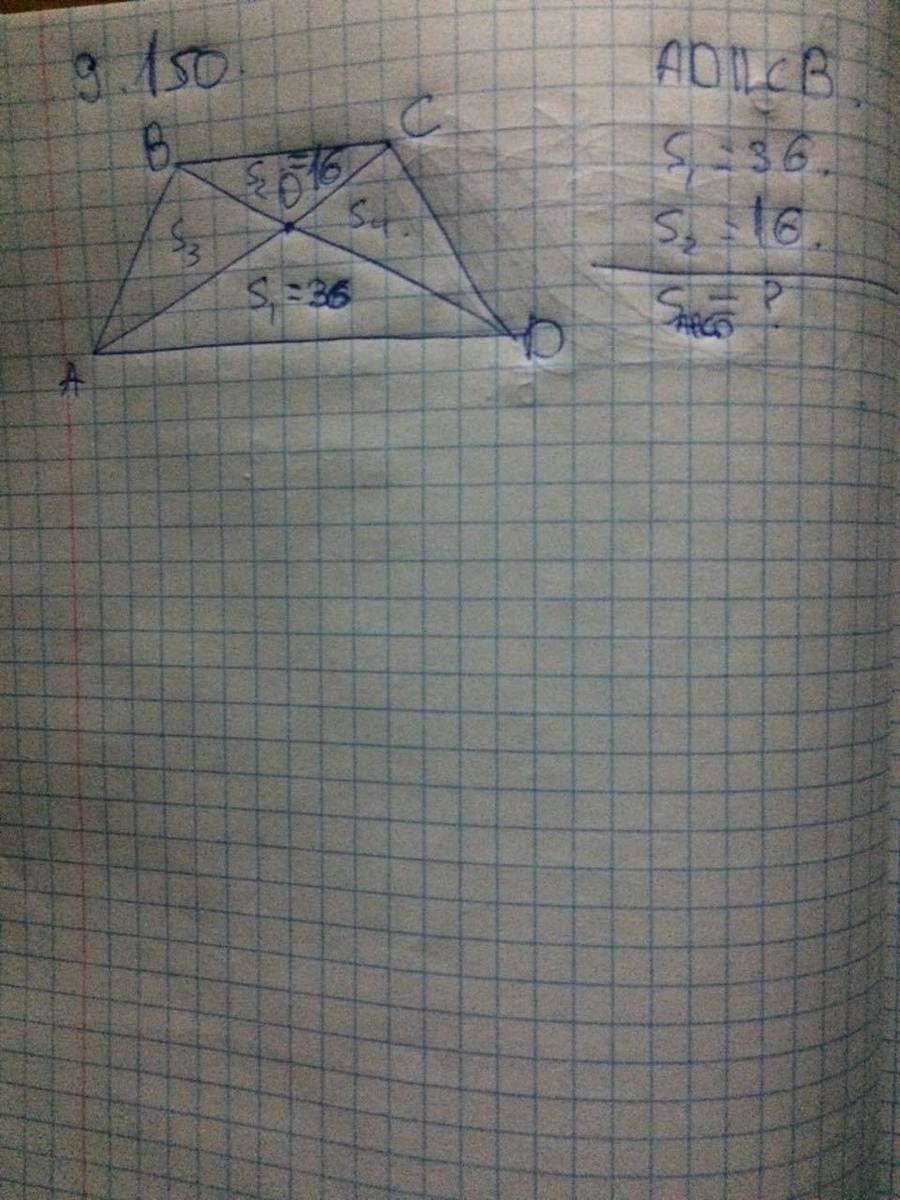
- Предмет:
  Геометрия
- Автор:
  toots17
- 6 лет назад

Ответы 4

спасибо тебе огромное ))) все точно как я хотел!
- Автор:
  joselynu3uo
- 6 лет назад
- 0
Там в конце наверное S= 1/2(AD+BC) а не DC.
- Автор:
  chiefoy7f
- 6 лет назад
- 0
Так и есть, ошибся!
- Автор:
  olive42
- 6 лет назад
- 0
Проведём высоту из основания BC к основанию AD так, чтобы она проходила через точку О и обозначим её EF. Площадь трапеции равна $S x_{ABCD}= \frac{1}{2}(AD+BC)*EF$ Треугольники BOC и AOD подобны (из свойств трапеции)Коэффициент подобия равен $\frac{AD^{2} }{BC^{2} }= \frac{S_{AOD} }{S_{BOC} }= \frac{36}{16}= \frac{9}{4}; \frac{AD}{BC}= \sqrt{ \frac{9}{4} }= \frac{3}{2}$ Значит и отношение высот треугольников BOC и AOD равно $\frac{OE}{OF}= \frac{2}{3} ; OE= \frac{2}{3}OF; OF= \frac{3}{2}OE$ $S_{BOC}= \frac{1}{2}BC*OE=16; BC*OE=32$ $S_{AOD}= \frac{1}{2}AD*OF; AD*OF=72$ Находим площадь трапеции $S_{ABCD}= \frac{1}{2}(AD+DC)*EF= \frac{1}{2}(AD*EF+BC*EF)$ = $= \frac{1}{2}(AD(OE+OF)+BC(OE+OF)=$ $= \frac{1}{2}(AD*OE+AD*OF+BC*OE+BC*OF)=$ $= \frac{1}{2}(AD*OE+72+32+BC*OF)=$ $= \frac{1}{2}(104+AD* \frac{2}{3}OF+BC* \frac{3}{2}OE)=$ $= \frac{1}{2}(104+ \frac{2}{3}*72+ \frac{3}{2}*32)= \frac{1}{2}(104+48+48)=100$
- Автор:
  snuggleswv5b
- 6 лет назад
- 0
Добавить свой ответ