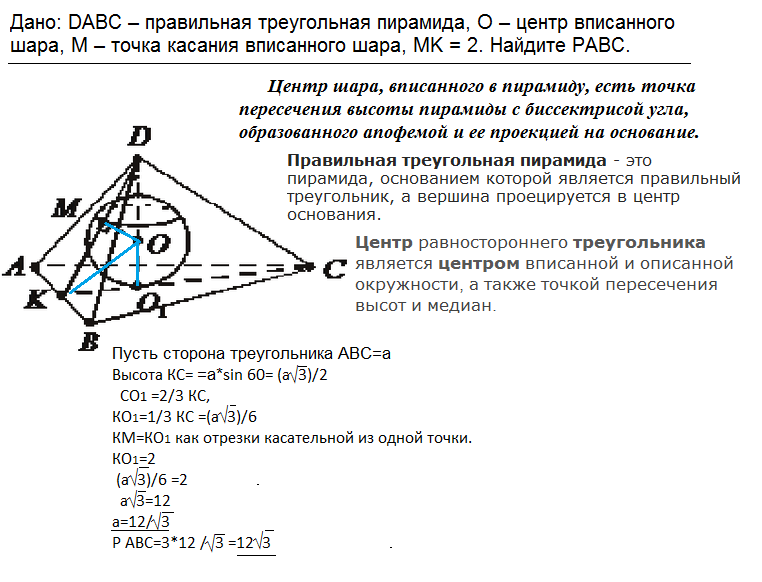
Дано: DABC – правильная треугольная пирамида, O – центр вписанного шара, M – точка касания вписанного шара, MK = 2. Найдите PABC.

Дано: DABC – правильная треугольная пирамида, O – центр вписанного шара, M – точка касания вписанного шара, MK = 2. Найдите PABC---- Вспомним несколько определений:    Правильная треугольная пирамида - это пирамида, основанием   которой является правильный треугольник, а вершина  проецируется в центр основания.     Центром равностороннего треугольника является  точка пересечения биссектрис, высот и медиан. Центр шара, вписанного в пирамиду, есть точка пересечения высоты пирамиды с биссектрисой угла, образованного апофемой и ее проекцией на основание.  Решение.      Пусть сторона ∆ АВС=а   Тогда высота КС=а*sin 60º   KC=a√3):2   КО₁=КС:3=a√3):6   КО₁=КМ=2 как отрезки касательных из одной точки. ⇒     a√3):6=2  a=12/√3    Р=3*12/√3    Р=12√3