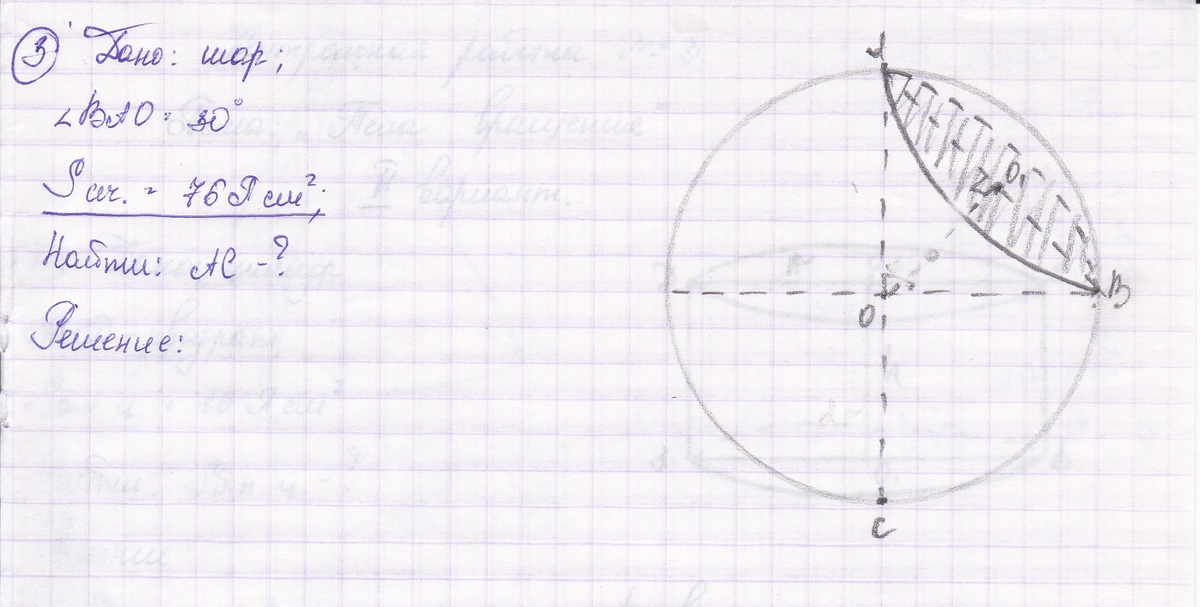
Площадь сечения шара плоскостью, проведенной через конец диаметра под углом 30 градусов к нему, равна 75п см^2. Найти диаметр шара.

  На данном Вами рисунке треугольник АОО1 - равнобедренный прямоугольный. Углы при диаметре сечения в рисунке равны. Обойдемся без него. 

------------------------------------------------------------------------------Смотрим на схематический  рисунок, данный во вложении к задаче. АС- диаметр шара и равен двум его радиусам.  

АВ- диаметр сечения, также равен двум радиусам сечения. Диаметр шара можно определить из прямоугольного треугольника АВС, где угол В - прямой, т.к угол АВС опирается на диаметр АС,

АС - гипотенуза, и

АВ - больший катет этого треугольника. Так как угол САВ равен 30°, диаметр АС шара равен диаметру АВ сечения, деленному на косинус 30 градусов. Диаметр сечения равен двум радиусам, которые можно найти из площади этого сечения. S=πr²r²=S:πr²= 75 π:π=75 см²r= 5√3 смДиаметр АВ сечения =2r =10√3 смАС=АВ:cos( 30°) =10√3:{(√3):2}=20√3):√3=20  см