-
Решение задач по готовым чертежам)
11,12,15,16)
Желательно с ДАНО.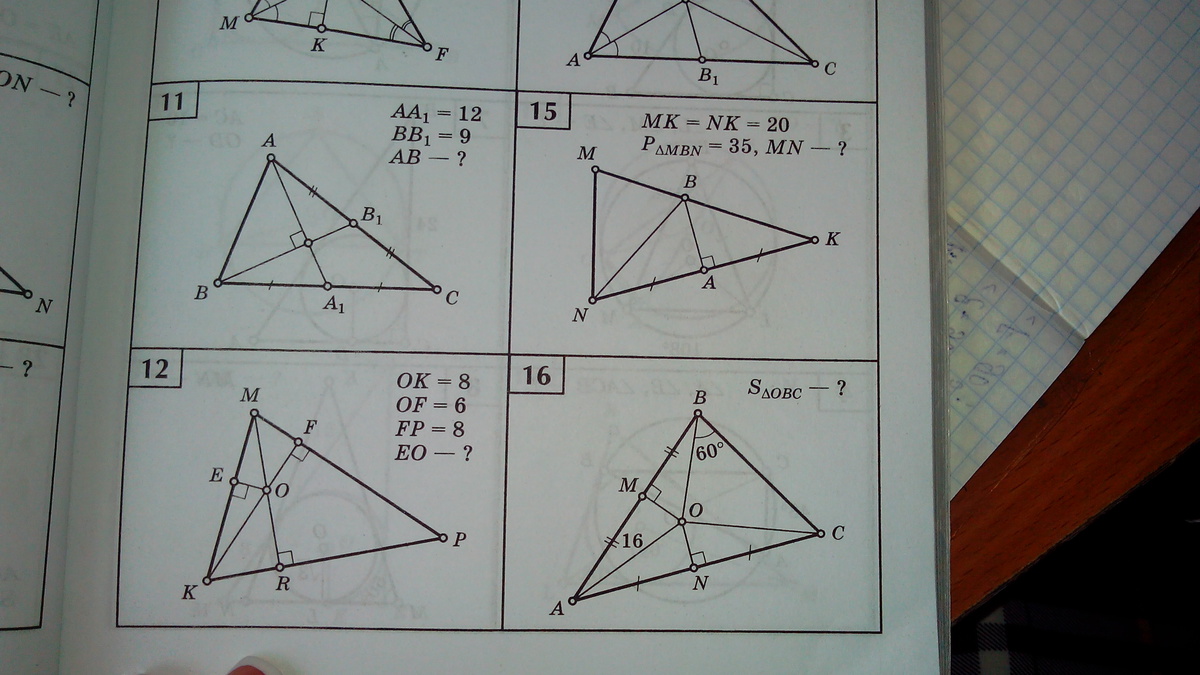
-
Предмет:
Геометрия -
Автор:
madilynnibarra - 6 лет назад
-
Ответы 1
-
№11. Дано: AA₁ - медиана AA₁ = 12 BB₁ - медиана BB₁ = 9 ∠AOB₁ = 90°Найти: АВРешение: Т.к. АА₁ и ВВ₁ - медианы, то точкой пересечения они делятся в соотношении 2 : 1. АО/ОА₁ = 8/4 ВО/ОВ₁ = 6/3 ∠АОВ = 90° АВ = √(АО² + ОВ²) = √(64 + 36) = 10Ответ: 10№16Дано: OM - медиана и высота ON - медиана и высота AO = 16 ∠OBC = 60°Найти: S ΔOBCРешение: АО = ОВ = ОС = 16 Проведём из т.О высоту (которая будет являться и медианой) OP. ∠OPB = 90°, ∠OBC = ∠OBP = 60°, => ∠BOP = 180° - 90° - 60° = 30° Против угла в 30° лежит сторона, равная половине гипотенузы. BP = 1/2 OB = 1/2 * 16 = 8 BP = PC = 8 BC = BP + PC = 16 S ΔOBC = 1/2 * OB * BC * sin∠OBC = 1/2 * 16 * 16 * √3/2 S ΔOBC = 64√3Ответ: 64√3
-
Автор:
valentina80 - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Решите пример, пожалуйста.
3x-2-3(x+5)=-(2-x)-5
-
Решите задачу и составьте для неё решетку Пеннета
Резус-положительная женщина со второй группой крови, отец которой имел резус-отрицательную кровь первой группы, вышла замуж за резус-отрицательного мужчину с первой группой крови. Какова вероятность, что ребенок унаследует оба признака от отца? -
я, кстати, спрашивал у Марь Иванны, она у нас будет вести профиль по английскому, она сказала, что мы не будет просто так проходить учебник, будем постигать что-то новое, дополнительное.
=-=-=-=-=-=-=-=-
Правильно ли здесь расставлены запятые?-
Предмет:
Русский язык -
Автор:
bowman - 6 лет назад
-
Ответов:
0 -
Смотреть
-
- Какие перья у вороны, голубя и глухаря. Если есть ответ, то почему.
How much to ban the user?
1 hour
1 day
100 years
