-
Помогите,пожалуйста
Доказать что треугольник ABC равнобедренный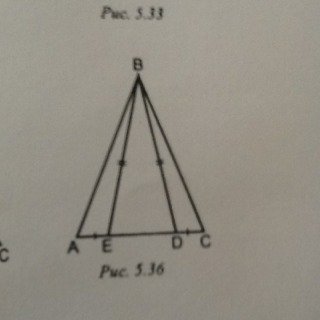
Ответы 1
-
Рассмотрим треугольник ВЕД. Так как его боковые стороны равны, что указанно на чертеже, то он равнобедренный, из чего следует равенство двух его углов при основании - ВЕД И ВДЕ.Рассмотрим треугольники ВАЕ И ВДС. АЕ=ДС (по условию)ВЕ=ВД (по условию)Угол АЕД = 180°- угол ВЕДУгол ВДС = 180° - угол ВДЕ, 180°=180°, угол ВЕД = уголу ВДЕ, ⇒ угол АЕД = углу ВДС, ⇒Треугольники ВАЕ И ВДС равны по двум сторонам и углу между ними.Из этого равенство следует равенство сторон АВ И ВС, А ТАК КАК ОНИ РАВНЫ, ТО МОЖНО ЗАКЛЮЧИТЬ, ЧТО ТРЕУГОЛЬНИК АВС -РАВНОБЕДРЕННЫЙ. Что и требовалось доказать.
-
Автор:
jayvon - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
- Северная Америка . Особенности географического положения и природы материка .
-
Заполните таблицу <<Этапы эволюции многоклеточных растений и животных>>
Помогите пожалуйста =^_^= -
Назови все векторы,
противоположно направленные для вектора BK−→− -
БАЛЛЫ!!!!! 40!!!!!
положение казачества в пореформенный период-
Предмет:
История -
Автор:
madilynuqah - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
