помогите пожалуйста если можно фото заранее спасибо

СПАСИБООО!!!

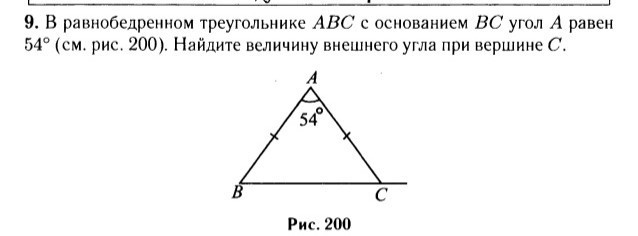
по рисунку мы видим , что это равнобедренный треугольник .Углы при Основании Равнобедренного треугольника . угл АВС= углу АСВ. Сумма внутренних углов треугольника = 180° . 180-(54+2х) 2х=180-542х= 126 х = 63 -это углы при основании треугольника ( АВС и АСВ )т.к.нужен внешний угол С , он смежен с АСВ . Сумма смежных углов = 180° 180-63= 117 °

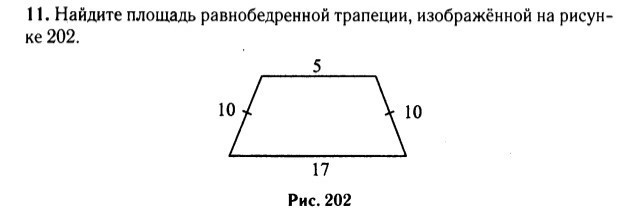
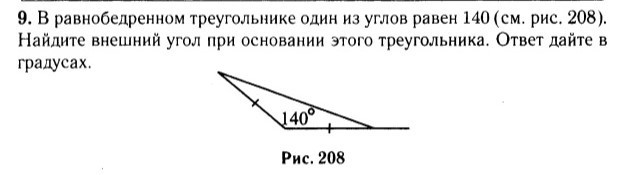
Рисунок 1. Сумма углов треугольника равна 180°, то есть ∠А+∠В+∠С=180° или 54°+∠В+∠С=180°∠В+∠С=180°-54°=126°Так как ∠В и ∠С в равнобедренном треугольнике равны, то ∠В=∠С=126:2=63°Внутренний угол треугольника АВС при вершине С и внешний угол треугольника при этой же вершине образуют развёрнутый угол, который равен 180°. Значит чтобы найти внешний угол надо от 180° отнять внутренний угол:180°-63°=117°Ответ: внешний угол при вершине С равен 117°Рисунок 2. Обозначим трапецию как АВСD, где AD и ВС основания, а АВ и CD боковые стороны, ВF - высота. Формула площади трапеции:S=((AD+BC)/2)*BFНам неизвестна высота, её можно найти по теореме Пифагора:BF²=AB²-AF²Отрезок АF находим из свойств равнобедренной трапеции, АF равен полуразности оснований трапеции:АF=(AD-BC)/2=(17-5)/2=12/2=6BF=√(10²-6²)=√(100-36)=√64=8Теперь можем найти площадь:S=((17+5)/2)*8=(22/2)*8=11*8=88 ед²Ответ: площадь трапеции 88 ед²Рисунок 3. Задача такая же как и в первом рисунке, поэтому расписывать не буду. Сумма углов треугольника равна 180°, углы при основании равнобедренного треугольника равны, поэтому180°-140°=40°40:2=20°Сумма смежных углов равна 180° следовательно180°-20°=160°Ответ: внешний угол при основании треугольника равен 160°