-
В равнобедренном тупоугольном треугольнике ABC на продолжение боковой стороны BC опущена высота AH. Из точки H на сторону AB
и основание AC опущены перпендикуляры HK и HM соответственно.
а) Докажите, что отрезки AM и MK равны.
б) Найдите MK, если AB=5, AC=8.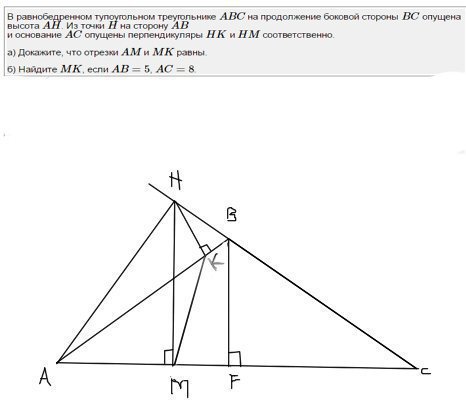
Ответы 1
-
В равнобедренном тупоугольном треугольнике АВС на продолжение боковой стороны ВС опущена высота АН. Из точки Н на сторону АВ и основание АС опущены перпендикуляры НК и НМ соответственно.
а) Докажите, что отрезки АМ и МК равны.
б) Найдите МК, если АВ=5, АС=8
Сделаем чертеж.
АН - высота тупоугольного треугольника, проведенная к боковой стороне, и расположена вне треугольника; угол АНС прямой.
⊿ АНС - прямоугольный, НМ⊥АС, и по свойству высоты прямоугольного треугольника делит его на подобные треугольники АМН и СМН.
∠АНМ=∠ВСА (=∠ВАС, т.к. углы при основании равнобедренного треугольника равны)
⊿ АМН и ⊿ АКН прямоугольные и имеют общую гипотенузу АН, следовательно, вокруг них можно описать общую окружность с диаметром АН.
В этой окружности вписанные углы АНМ и АКМ по свойству вписанных углов, опирающихся на одну дугу, равны. ⇒
∠АКМ=∠АНМ, но ∠АНМ=∠ВСА= ВАС ⇒
∠АКМ=∠КАМ, ∆ АМК равнобедренный, и АМ=КМ, что и требовалось доказать.
--------------
б) Найдите МК, если АВ=5, АС=8
МК=АМ. Найдем длину АМ.
Так как ∆ АВС равнобедренный, высота ВТ в нем и биссектриса и медиана. ⇒
АТ=ТС=8:2=4
В ⊿ ВТС отношение катета ТС и гипотенузы ВС =4:3,⇒ он- египетский, и ВТ=3 ( то же и по т.Пифагора)
sin ∠ВСТ=ВТ:ВС=0,6
АН=АС•sin∠ACH=8•0,6=4,8
Т.к. ∠АНМ=∠ВСА ( доказано из подобия), то
АМ=АН•sin ∠АНМ
АМ=4,8•0,6=2,88
Следовательно, и МК, равный АМ, равен 2,88 (ед. длины)

-
Автор:
biscuithenderson - 6 лет назад
-
0
-
-
Добавить свой ответ
-
Запишите систему органов человека
-
Предмет:
Обществознание -
Автор:
english90 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Talk to your friend. 1 What’s your name? 2 What time do you come to school? 3 What time do you have breakfast? 4 What time do you have lunch? 5 What’s your favourite food? 6 Are you hungry? 7 What do you want to eat? 8 Are you thirsty? 9 What do you want to drink? как на них ответить правильно
-
Предмет:
Английский язык -
Автор:
jackr6ku - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
как написать смешное сочинения про жару
-
Предмет:
Литература -
Автор:
baldwin - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
в одной корзине 7 брюкв а во второй 5 таких же брюкв Вычислите массу брюквы в каждой корзине если известно что масса первой корзины на 1 килограмм больше чем масса 2 корзины
-
Предмет:
Математика -
Автор:
probocortez - 6 лет назад
-
Ответов:
1 -
Смотреть
-
