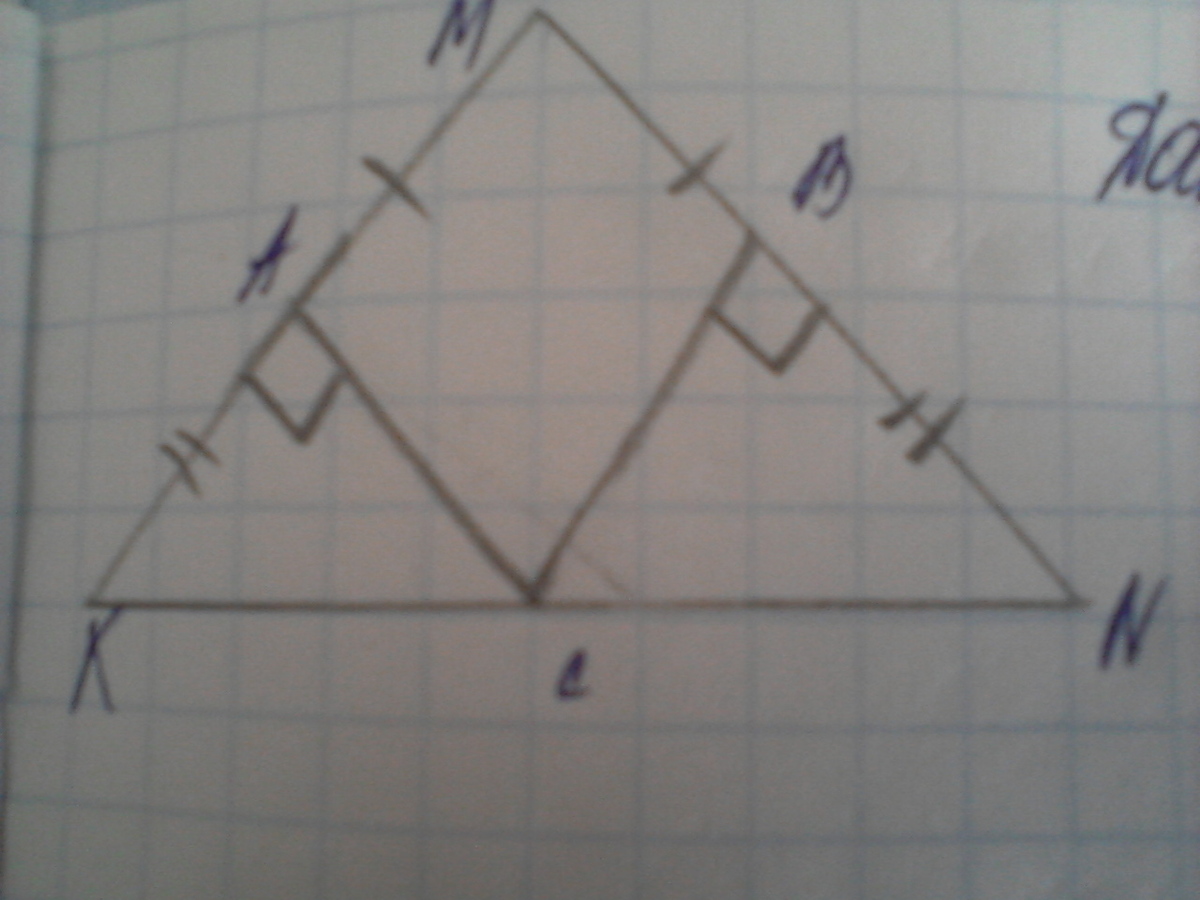
дано: треугольник KMN, AK=BN, AM=BM, CA перпендикулярно KM, CB перпендикулярно NM

доказать: MC - медиана треугольника KMN

дано: треугольник KMN, AK=BN, AM=BM, CA перпендикулярно KM, CB перпендикулярно NMдоказать: MC - медиана треугольника KMN В треугольнике KMN боковые стороны состоят из равных отрезковAK=BN, AM=BM, следовательно

КМ=МК+АМ=ВN+MB=MN

Треугольник KMN - равнобедренный.

Δ КАС=Δ СВN,

так как это прямоугольные треугольники,

углы К и N равны как углы при основании равнобедренного треугольника,

катеты КА=ВN. Если в прямоугольном  треугольнике  острый угол и катет равен острому углу и катету другого прямоугольного треугольника, то эти треугольники равны.

Следовательно, гипотенузы АС и CN этих треугольников равны.АС=СN Точка С - середина стороны КNМС - медиана треугольника KMN, что и требовалось доказать.