-
Точка С - середина отрезка AB, не пересекающего плоскость альфа.
Через точки А, С и B проведены параллельные прямые, пересекающие плоскость альфа, соответственно в точках А1, С1, B1. Докажите что точки А1, С1, B1 лежат на одной прямой. Найдите СС1, если АА1=5см, BB1 = 7 см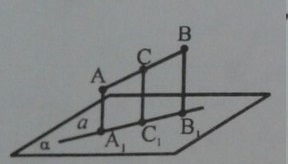
Ответы 1
-
АА₁ || ВВ₁ , АВ∦(не параллельно) А₁В₁ ⇒ А₁АВВ₁ - трапеция
АС = СВ, АА₁ || СС₁ || ВВ₁ ⇒ А₁С₁ = С₁В₁ - по теореме Фалеса
Точка С₁ - середина А₁В₁, значит, точки А₁ , С₁ и В₁ лежат на одной прямой
Или можно пойти от противного, допустим точка С₁ ∉ А₁В₁ , С₁ ∈ α, тогда если провести среднюю линию СМ трапеции А₁АВВ₁, А₁М = МВ₁, то АА₁ || СМ || ВВ₁ , но по условию АА₁ || СС₁ || ВВ₁ ⇒ СМ || СС₁, что невозможно, а значит, точка С₁ ∈ А₁В₁ , ч.т.д.
АС = СВ, А₁С₁ = С₁В₁ ⇒ СС₁ - средняя линия
СС₁ = (АА₁ + ВВ₁)/2 = (5 + 7)/2 = 6 см
Ответ: 6 см

-
Автор:
dorkdcsu - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Шляпа красивая - это словосочентание ? Меня смущает порядок слов.
-
Предмет:
Русский язык -
Автор:
rhysbeasley - 6 лет назад
-
Ответов:
3 -
Смотреть
-
-
помогите составить предложения со схемами 1) в конце каждого предложения [ ].[ ]! [ ]?, 2) 3 сложных предложений [ ],[ ]. [ ],и [ ], [ ], [что] 3) 4 предложения где есть однородные члены [ 0 и 0 ], [0,0 и 0], [0:0.0]. [0.0и 0-0]
-
Предмет:
Русский язык -
Автор:
jettazkys - 6 лет назад
-
Ответов:
3 -
Смотреть
-
-
. Упростите заданное алгебраическое выражение. Вычислите его значение при y=4/17.
54−2∗(7y+3)−(3y+4).
-
Предмет:
Алгебра -
Автор:
makenahorne - 6 лет назад
-
Ответов:
0 -
Смотреть
-
-
Как превратить: а) ненасыщенный раствор в насыщенный; б) насыщенный раствор в ненасыщенный.
-
Предмет:
Химия -
Автор:
persyfrederick - 6 лет назад
-
Ответов:
0 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
