Найти углы/стороны. 9 класс. Требуется краткое решение, без всяких рассмотрим. Ответы знаю

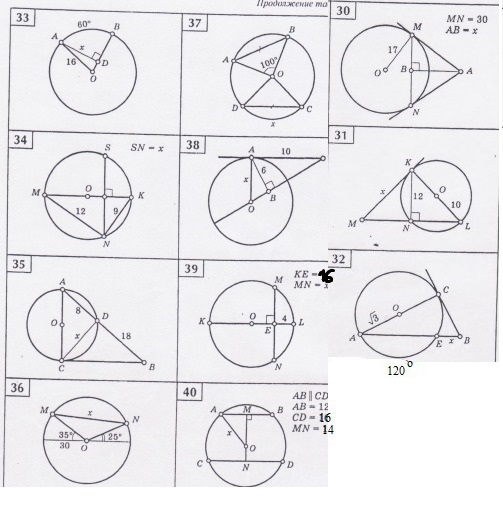
34) Угол MNK прямой, как опирающийся на диаметр.Тогда МК = √(12²+9²) = √(144+81) = √225 = 15.Обозначим точку пересечения МК и SN за Е.Пусть отрезок EK = у, а ME = 15-у.По свойству высоты NE в прямоугольном треугольнике MNK:.Заменим  МЕ и ЕК:Отсюда у = 1215/225 = 5,4.Тогда искомый отрезок SN = 2√(9²-5,4²) = 2√51,84 = 14,4.36) Угол MON = 180°-35°-25° = 120°.Отрезки MO и NO это радиусы длиной 30.Длина отрезка MN равна:MN = 2Rsin(120°/2) = 2*30*(√3/2) = 30√3.40) Обозначим ОМ = у, а ON = 14-у, радиус за х.Из треугольников АОМ и ОСN выразим неизвестный радиус:х² = (12/2)²+у²,х² = (16/2)²+(14-у)².Приравняем правые части уравнений:36+у² = 64+196-28у+у².28у = 224.у = 224/28 = 8.Тогда радиус равен √(6²+8²) = √(36+64) = √100 = 10.30) Находим ОВ = √(17²-(30/2)²) = √289-225) = √64 = 8.По свойству высоты ВМ в прямоугольном треугольнике:8/15 = 15/АВ, отсюда АВ = 15*15/8 = 28,125.

30MB=1/2*MN=15OB=√(OM²-MB²=√289-225=√64=8OM²=OB*OAOA=OM²/OB=289/8AB=OA-OB=289/8-8=(289-64)/8=225/8=28,12534MK=√MN²+NK²=√(144+81=√225=15NK²=KD*MK,D-точка пересечения MS и MKKD=NK²/MK=81/15ND=√NK²-KD²=√81-81²/15²=√81(225-81)/225=9*12/15=36/5=7,2NS=2ND=14,436<MON=180-(35+25)=180-60=120MN²=OM²+ON²-2OM*ON*cos120=900+900-2*900*(-1/2)=3*900MN=30√340AM=1/2*AB=6CN=1/2*CD=8AO=OC=xON=y  OM=14-yAO²=AM²+OM²=CN²+ON²x²=36+(14-y)²=64+y²36+196-28y+y²=y²+6428y=232-6428y=168y=168:28y=6x²=64+36x²=100x=10AO=10