-
Пожалуйста, помогите решить задачу!
Длина ребра куба АBCDA1B1C1D1 равна 8 дм.Точка О - точка пересечения диагоналей грани ABCD(рис.б).Вычислите площадь диагонального сечения пирамиды OA1B1C1D1.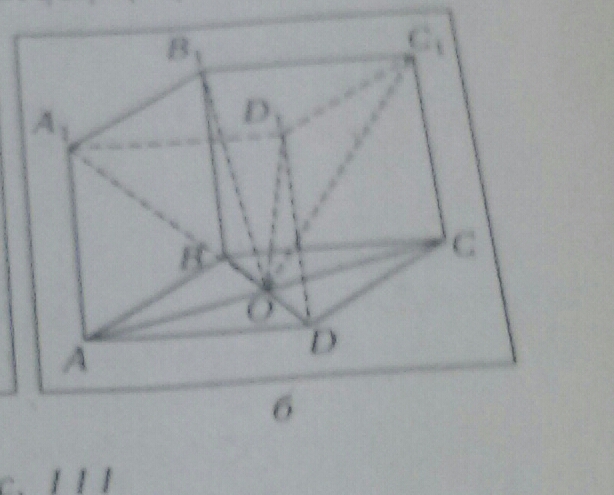
Ответы 1
-
Диагональ А1С1 по теореме Пифагора 8²+8²=А1С1², А1С1=√(2*64)=8√2Из треугольника ОСС1 находим ОС1, СС1=8 по условию, ОС - половина диагонали. ОС1=√(64+(2√2)²)=√(64+8)=√72=6√2. Высота пирамиды и соответственно треугольника ОСС1 будет равна боковому ребру и = 8. Площадь = 1/2 * 4√2 * 8=16√2
-
Автор:
consueloruiz - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Точто под значком пожалуйста
-
Предмет:
Русский язык -
Автор:
lucapowers - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
допоможіть написати. твір 12 речень про своє місто на англійській мові
-
Предмет:
Английский язык -
Автор:
laddie - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
сочно нужна помощь!!!!!!!!!!!
сократите дробь
4 в 5 степени * 4 в 7 степени/ 4 в 14 степени
б) х в квадрате + 6ху + 9 у в квадрате/ х в квадрате - 9у в квадрате -
Какой корень в слове создавали
-
Предмет:
Русский язык -
Автор:
jeremyq7ew - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
