-
МНОГО БАЛЛОВ ДАМ ЗА РЕШЕНИЕ ЭТОЙ ЗАДАЧИ)
Дано: ABCD - параллелограмм, AN-биссектриса ∠BAD, BM-биссектриса ∠ABC.
Доказать: ABNM-параллелограмм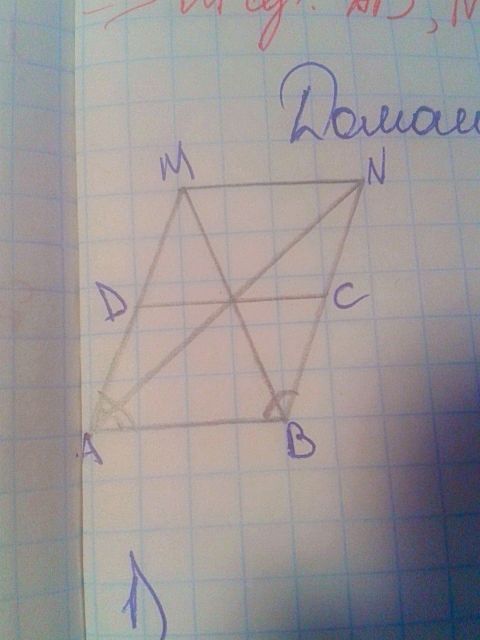
-
Предмет:
Геометрия -
Автор:
lorenzobjnj - 6 лет назад
-
Ответы 1
-
∠АМВ=∠МВN как накрест лежащие при параллельных АМ и ВN и секущей ВМ. ВМ - биссектриса, значит ∠МВN=∠АВМ.В тр-ке АВМ ∠АМВ=∠АВМ, значит он равнобедренный с равными сторонами АВ и АМ.∠MAN=∠ANB как накрест лежащие при параллельных АМ и ВN и секущей АN. AN - биссектриса, значит ∠MAN=∠NAB.В тр-ке АNB ∠ANB=∠NAB, значит он равнобедренный. АВ=ВN.AM=AB=BN.AM║BN, AM=BN, значит АВ║MN, значит ABMN - параллелограмм.Доказано.Более того, так как диагонали АN и ВМ - биссектрисы, то АВNM - ромб.
-
Автор:
beef - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
мама может сделать уборку за 2 часа, а ее дочь за 3 часа. За сколько времени мама и дочь могли бы вместе убрать квартиру.
-
Предмет:
Математика -
Автор:
hilariónjvb3 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
а) 4x³·(-2x²)²
б) (a-4)·(a-8)+3a·(2a-6)
в) (x-3)·(x+3)-(x-2)²
Прошу очень помогите(( Мне надо умоляю-
Предмет:
Математика -
Автор:
gina - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
как правильно долина или далина роз,вдали или вдоли,издалека или издолека,удолиться или удалиться.
-
Предмет:
Математика -
Автор:
aubreyramirez - 6 лет назад
-
Ответов:
0 -
Смотреть
-
-
ABCD прямокутник периметр abcd=20 см AB= 7 см (плиз, кр)
-
Предмет:
Геометрия -
Автор:
mastera5z2 - 6 лет назад
-
Ответов:
2 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
