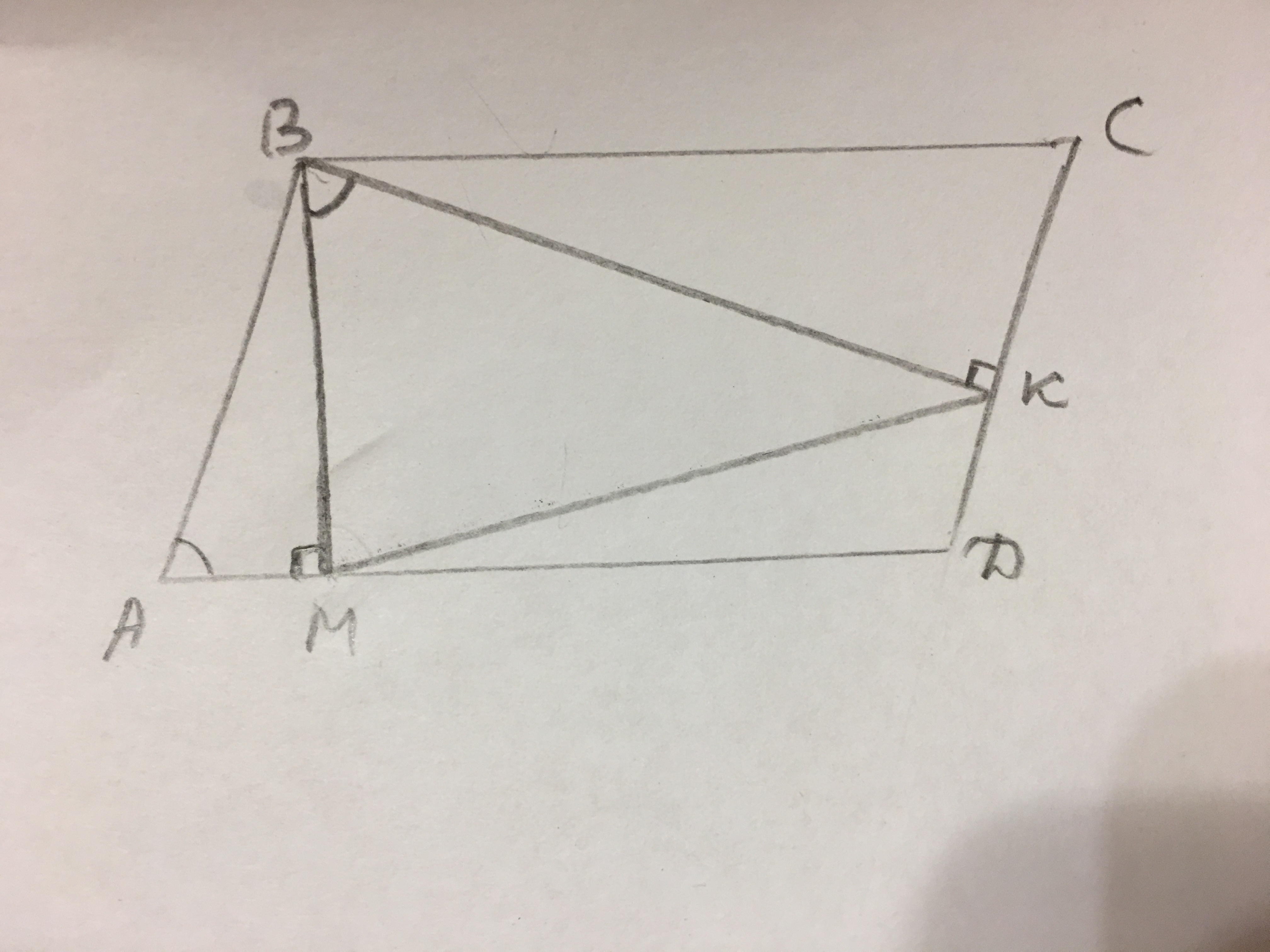
Из вершины тупого угла параллелограмма опущены высоты на его стороны, расстояния между основаниями которых равно 52 см. Определить стороны параллелограмма, если его высоты равны 56 см и 60 см.

В параллелограмме АВСД ВМ и ВК - высоты. ВМ=56 см, ВК=60 см, КМ=52 см.Углы между соответственно перпендикулярными прямыми равны.ВМ⊥АД, ВК⊥СД, значит ∠МВК=∠ВАД.В треугольнике ВМК по теореме косинусов cos(∠МВК)=(ВМ²+ВК²-КМ²)/(2·ВМ·ВК)=(56²+60²-52²)/(2·56·60)=0.6.sin²α=1-cos²α.sin²(∠ВАД)=1-0.6²=0.64,sin(∠ВАД)=0.8.Пусть АВ=х, АД=у.Площадь параллелограмма: S=ху·sinα=0.8ху.Также S=х·ВК=60х и S=у·ВМ=56у.1) 0.8ху=60х,у=60/0.8=75.АД=75 см - это ответ.2) 0.8ху=56у,х=56/0.8=70.АВ=70 см - это ответ.