СРОЧНОООО!!!!!!!!
В трапеции АВСД, ВС:АД=1:2. Е - середина боковой стороны СВ, точка М лежит на АЕ, так что АМ:МЕ=4:1.Используя векторы, докажите, что точка М лежит на диагонали ВД.

Ответ:

ОПИСКА  в условии. Дано решение для измененного условия.

Объяснение:

Условие: В трапеции АВСD, ВС:АD=1:2. Е - середина боковой стороны СВ, точка М лежит на АЕ, так что АМ:МЕ=4:1. Используя векторы, докажите, что точка М лежит на диагонали ВD.

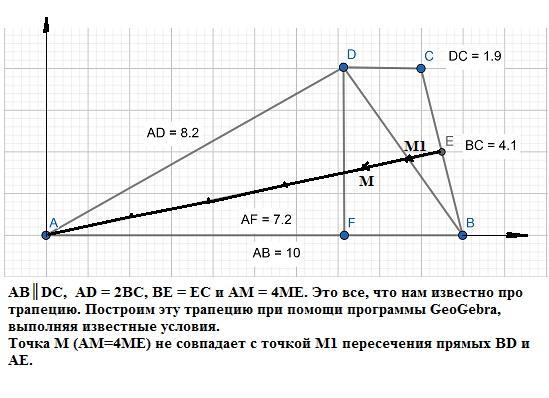
Сначала докажем, что в условии - опечатка. При таком условии (Е - середина боковой стороны СВ) точка М в общем случае не лежит на диагонали BD (приложение 1 и 4).

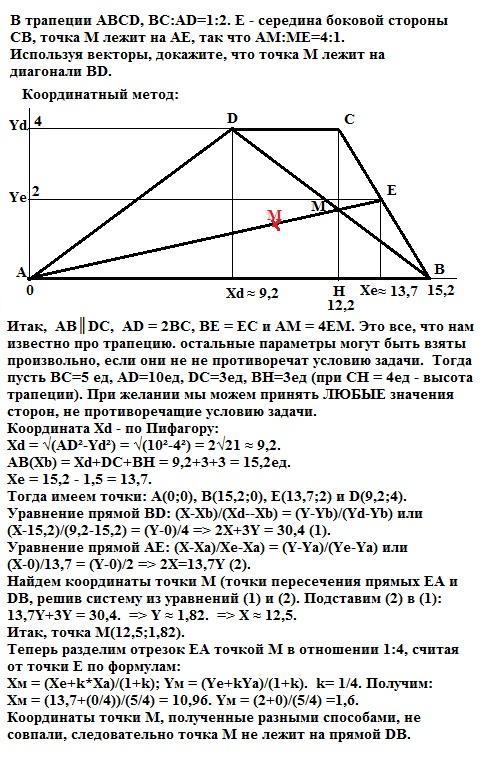
Итак,  АВ║DC,  AD = 2BC, ВЕ = ЕС и АМ = 4ЕМ. Это все, что нам известно про трапецию. остальные параметры могут быть взяты произвольно, если они не не противоречат условию задачи.  Тогда пусть ВС=5 ед, AD=10ед, DC=3ед, BH=3ед (при СН = 4ед - высота трапеции). При желании мы можем принять ЛЮБЫЕ значения сторон, не противоречащие условию задачи.

Координата Xd - по Пифагору:

Xd = √(AD²-Yd²) = √(10²-4²) = 2√21 ≈ 9,2.

АВ(Xb) = Xd+DC+BH = 9,2+3+3 = 15,2ед.  

Xe = 15,2 - 1,5 = 13,7.

Тогда имеем точки: А(0;0), В(15,2;0), Е(13,7;2) и D(9,2;4).

Уравнение прямой ВD: (X-Xb)/(Xd--Xb) = (Y-Yb)/(Yd-Yb) или

(Х-15,2)/(9,2-15,2) = (Y-0)/4 => 2X+3Y = 30,4 (1).

Уравнение прямой АE: (X-Xa)/Xe-Xa) = (Y-Ya)/(Ye-Ya) или (Х-0)/13,7 = (Y-0)/2 => 2X=13,7Y (2).

Найдем координаты точки М (точки пересечения прямых ЕA и DB, решив систему из уравнений (1) и (2). Подставим (2) в (1): 13,7Y+3Y = 30,4.  => Y ≈ 1,82.  => X ≈ 12,5.

Итак, точка М(12,5;1,82).

Теперь разделим отрезок ЕА точкой М в отношении 1:4, считая от точки Е по формулам:

Xм = (Хe+k*Xa)/(1+k); Yм = (Ye+kYa)/(1+k). Получим:

Xм = (13,7+(0/4))/(5/4) = 10,96. Yм = (2+0)/(5/4) =1,6.

М(10,96;1,6).

Координаты точки М, полученные разными способами, не совпали, следовательно точка М не лежит на прямой DB.

=======================================

Изменим условие:

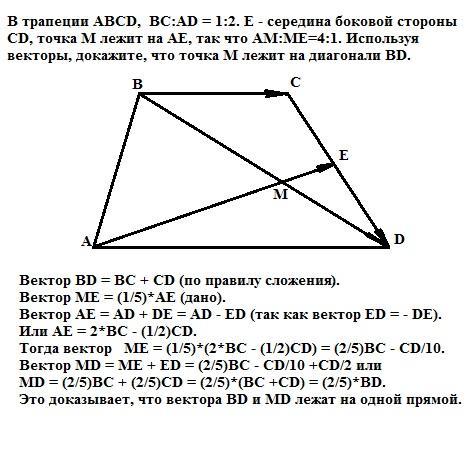
В трапеции АВСD,  ВС:АD = 1:2. Е - середина боковой стороны СD, точка М лежит на АЕ, так что АМ:МЕ=4:1. Используя векторы, докажите, что точка М лежит на диагонали ВD.

Доказательство (приложение 2):

Вектор BD = BC + CD (по правилу сложения).

Вектор МЕ = (1/5)*АЕ (дано).

Вектор АЕ = AD + DE = AD - ED (так как вектор ED = - DE).

Или АЕ = 2*ВС - (1/2)CD.

Тогда вектор   МЕ = (1/5)*(2*ВС - (1/2)CD) = (2/5)ВС - СD/10.

Вектор MD = ME + ED = (2/5)ВС - СD/10 +CD/2 или

MD = (2/5)ВС + (2/5)СD = (2/5)*(BC +CD) = (2/5)*BD.

Это доказывает, что вектора BD и MD лежат на одной прямой. Следовательно, точка М лежит на диагонали BD, что и требовалось доказать.

=======================================

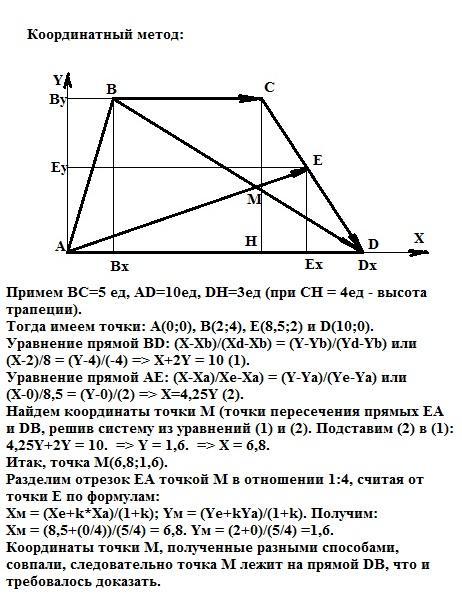
Метод координат (приложение 3):

Пусть трапеция АВСD c основаниями AD и ВС. Привяжем систему координат к вершине A так, что вектор AD лежит на оси Х в положительном направлении. Так как из условия нам известно только то, что AD=2*BC и точка Е - середина стороны CD, примем значения сторон трапеции так, что

ВС=5 ед, AD=10ед, DH=3ед (при СН = 4ед - высота трапеции). При желании мы можем принять ЛЮБЫЕ значения сторон, не противоречащие условию задачи.

Тогда имеем точки: А(0;0), В(2;4), Е(8,5;2) и D(10;0).

Уравнение прямой ВD: (X-Xb)/(Xd-Xb) = (Y-Yb)/(Yd-Yb) или

(Х-2)/8 = (Y-4)/(-4) => X+2Y = 10 (1).

Уравнение прямой АE: (X-Xa)/Xe-Xa) = (Y-Ya)/(Ye-Ya) или (Х-0)/8,5 = (Y-0)/(2) => X=4,25Y (2).

Найдем координаты точки М (точки пересечения прямых ЕA и DB, решив систему из уравнений (1) и (2).

Подставим (2) в (1): 4,25Y+2Y = 10.  =>

Y = 1,6.  => X = 6,8.

Итак, точка М(6,8;1,6).

Разделим отрезок ЕА точкой М в отношении 1:4, считая от точки Е по формулам:

Xм = (Хe+k*Xa)/(1+k); Yм = (Ye+kYa)/(1+k). Получим:

Xм = (8,5+(0/4))/(5/4) = 6,8. Yм = (2+0)/(5/4) =1,6.

М(6,8;1,6).

Координаты точки М, полученные разными способами, совпали, следовательно точка М лежит на прямой DB, что и требовалось доказать.

P.S. В дополнение представлен рисунок, на котором с помощью программы GeoGebra построена трапеция по условию, данному в задании. На нем видно, что точка М1 пересечения прямых BD и АЕ и точка М, делящая отрезок АЕ в отношении 4:1,  не совпадают.