-
Решите, пожалуйста, 9,10 и 15 номера. Все расписывайте подробно. Еще лучше, если кинете фото с листа.
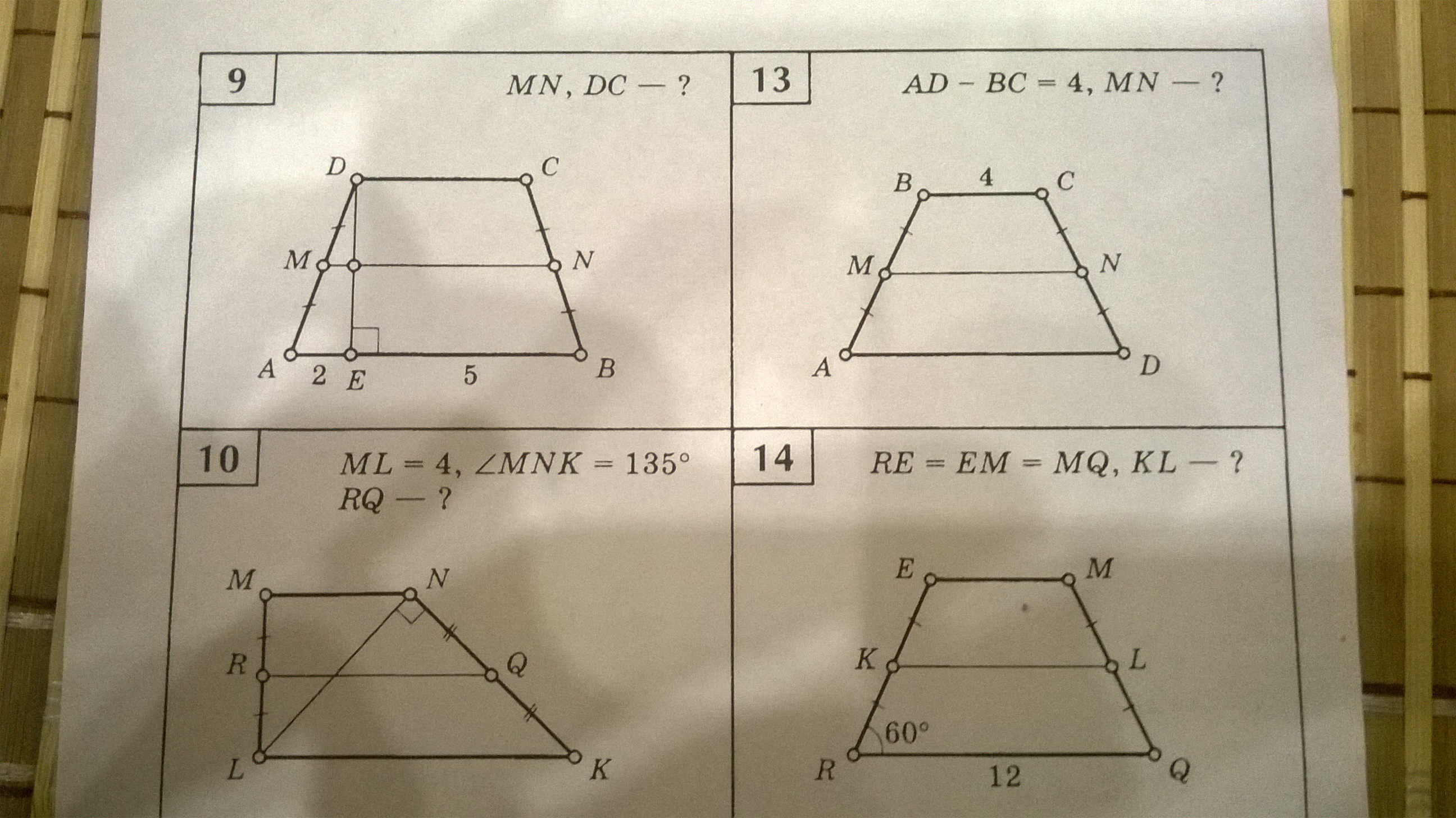
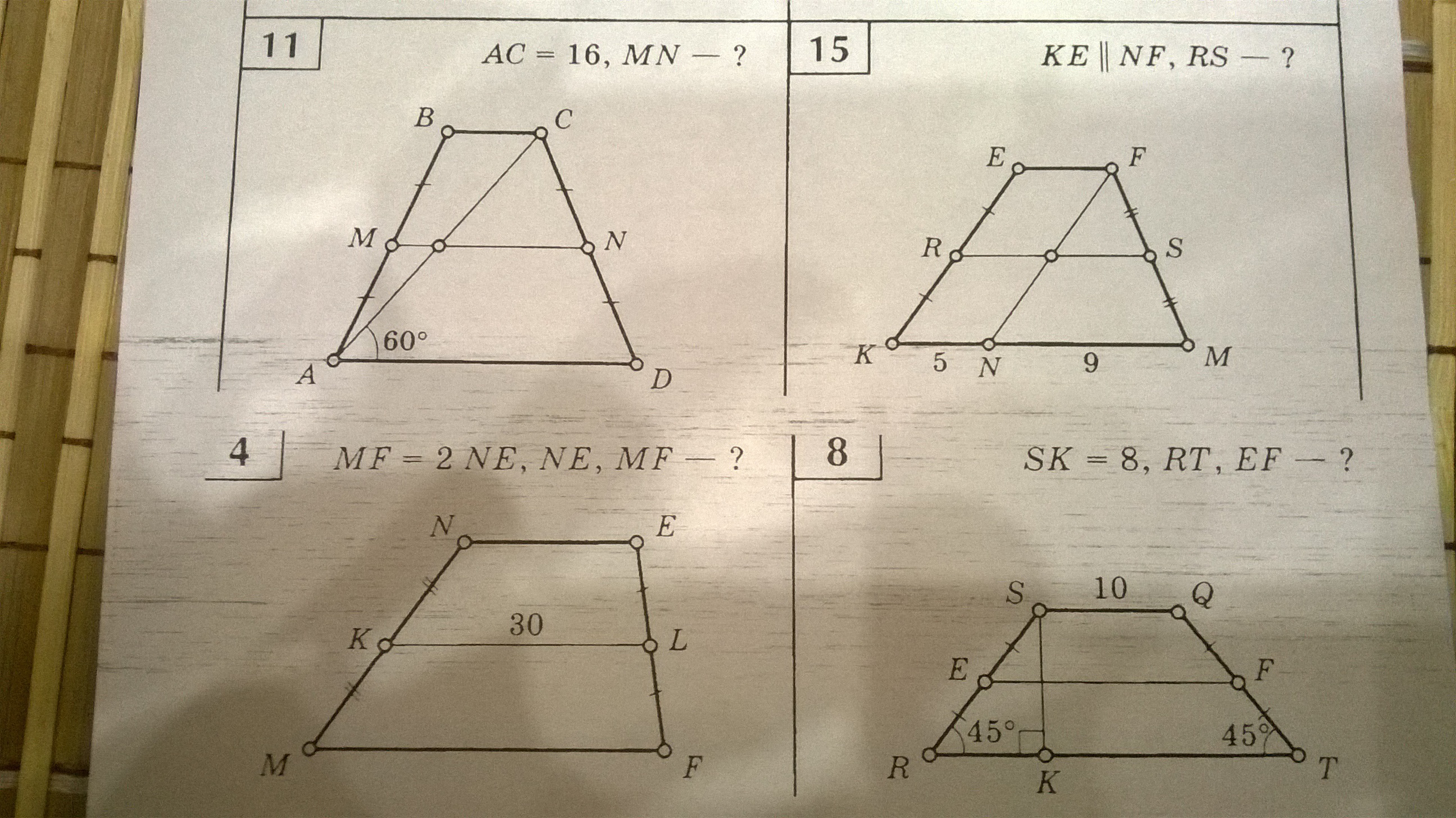
-
Предмет:
Геометрия -
Автор:
turkeycbjd - 6 лет назад
-
Ответы 1
-
В 9м трапеция ADCB равнобокая. Отмечено черточками равенство кусочков (половинок сторон). MN её средняя линия.Можно так из точки C на AB опустить высоту CH. Рассмотреть треуголники ADE и BHC поскольку трапеция равнобокая AD=CB∠A=∠B и ⇒ ∠ADE=∠BCH. (Хотя и высоты DE и CH тоже равны).В общем выбираем признак равенства треугольников, какой нравится. Можно например по одной стороне и 2м углам.ΔADE=ΔBHC ⇒ AE=BH=2EH=EB-BH=5-2=3EDCH -- прямоугольник DC=EH (противоположные стороны)Средняя линия MN=(DC+AB)/2=(3+7)/2=5В 10-м ∠MNL=135-90=45°∠NLK=∠MNL=45° как внутренние накрест лежащие при параллельных прямых MN, LK и секущей NL.Значит в ΔLNK ∠K=180-(90+45)=45°. Т.е. он получился прямоугольный (поусловию) равнобедренный (углы при основании LK равны). NL=NK.Вот не отмечено тут, и всё же, если угол ипри M не прямой, то однозначного решения нет, а если прямой, то ∠MLK=90, ∠MLN=90-45=45°. ΔLMN прямоугольный равнобедренный. MN=ML=4. LN находим по теореме Пифагора
Аналогично в ΔLNK находим гипотенузу LK (оно же одно из оснований трапеции).
Тогда средняя линия RQ=(LK+MN)/2=(8+4)/2=6

-
Автор:
carpenter - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
На 4,2 г лития подействовали 12г воды , найдите объем полученного газа.
-
Предмет:
Химия -
Автор:
francojttj - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
При каких значениях переменной имеет смысл выражения -3√5c ?
-
Предмет:
Алгебра -
Автор:
románquinn - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Даны рифмы. Вы должны сочинить стихотворения что бы была рифма. Стих должен быть связан с праздником хэллоуин .
1 рифма для 1 стиха - нос-вопрос.
2 рифма для 2 стиха - стакан-таракан.
Помогите пожалуйста!!!-
Предмет:
Литература -
Автор:
jacquelinejnwg - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
сочинение на тему "родина"
-
Предмет:
Русский язык -
Автор:
aaron55 - 6 лет назад
-
Ответов:
3 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
