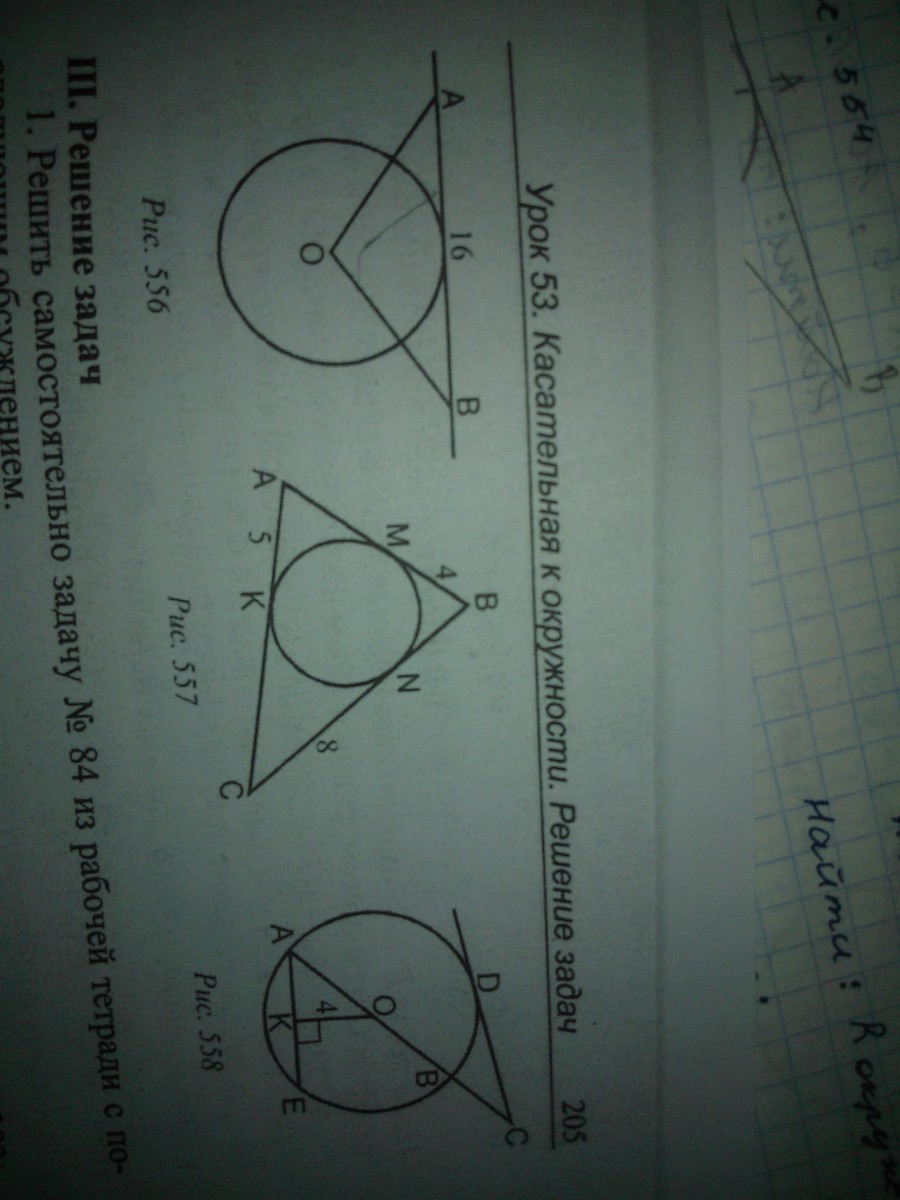
Касательная к окружности. Решение задач на готовых чертежах. 1)рис. 555; Дано:ab, bc - касательные, ob=2, ao=4. Найти: угол BOC. 2)рис. 556; Дано:ab - касательная, R=6, ao=ob. Найти: ao. 3)рис. 557;  Дано:М, N, K - точки касания. Найти: периметр ABC. 4)рис. 558; Дано:ab=10см, O - центр окружности, cd - касательная, ae параллельно cd. Найти: oc Помогите пожалуйста.

Угол BOC = 90°. Это следует из свойства касательной к окружности – отрезок, проведенный из точки касания прямой с окружностью до центра этой окружности, перпендикулярен этой прямой.

Ao=Ob=6, так как длина радиуса равна его радиусу.

Нет достаточных данных для вычисления периметра треугольника ABC. Для этого необходимо знать длины сторон, или их соотношение и одну из сторон, или одну из высот и соответствующую ей сторону, или радиус вписанной или описанной окружности и некоторые углы треугольника, или ряд других комбинаций.

Oc=5см. Это следует из свойства касательной, что отрезок, проведенный из точки касания прямой с окружности до центра этой окружности, перпендикулярен этой прямой. Таким образом, треугольник OAC - прямоугольный, и Oc является его гипотенузой, а следовательно, по теореме Пифагора Oc=√(Oa^2-Ac^2)=√(10^2-5^2)= √75=5√3.