-
Диагонали параллелограмма ABCD пересекаются в точке O. Биссектрисы углов OAD и CBO пересекаются в точке K. Найти величину угла AKB, если OCKD - параллелограмм.
Биссектрисы углов НЕ параллельны, а пересекаются за пределами параллелограмма.
Рисунок приблизительный~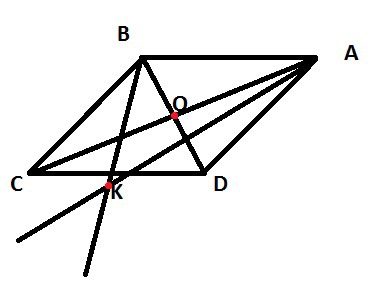
Ответы 1
-
Дано: ОСКD - параллелограмм.Если у четырехугольника пара противоположных сторон параллельны и равны, то четырехугольник – параллелограмм.Следовательно, АОКD и ВОКС - параллелограммы.Значит ВС=ОК=АD.Но ВК - биссектриса угла и диагональ параллелограмма ВОКС, отсюда ВС=СК=ВО. Тогда ВD=2ВС.С другой стороны АК - биссектриса угла и диагональ параллелограмма АОКD, отсюда АD=DK, но АD=ВС, значит DK=CK и ОСКD -ромб.Значит СD перпендикулярна ОК.Подкорректируем рисунок (рис.2)Тогда и ВС перпендикулярна СD и АВСD - прямоугольник, в котором диагонали равны удвоенной стороне ВС(АD).Из этого следует, что <BDC=<ACD=30°, а <СBD=<СAD=60°.ВК и АК - биссектрисы, значит <ABK = <BAK = 60°.Итак, в треугольнике АВК два угла при стороне АВ равны по 60°, следовательно и угол АКВ=60°.Ответ: угол АКВ = 60°.

-
Автор:
winstonr9lc - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
- князь который был убит за попытку вторично собрать дань с древлян
-
чем обьяснить взаимн непримеримость католиков и гугенотов
-
Предмет:
История -
Автор:
killianzlkf - 6 лет назад
-
Ответов:
1 -
Смотреть
-
- основное занятие древних славян
- столица государства, с которым был подписан договор, дающий русским купцам право беспошлинной торговли?
How much to ban the user?
1 hour
1 day
100 years
